Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T11:00:23.117Z Has data issue: false hasContentIssue false
  • English
  • Français

PERFECT POWERS THAT ARE SUMS OF TWO POWERS OF FIBONACCI NUMBERS

Part of: Diophantine equations

Published online by Cambridge University Press:  30 August 2018

ZHONGFENG ZHANG Open the ORCID record for ZHONGFENG ZHANG [Opens in a new window]  and
ALAIN TOGBÉ
ZHONGFENG ZHANG
Affiliation:
School of Mathematics and Statistics, Zhaoqing University, Zhaoqing 526061, China email bee2357@163.com
ALAIN TOGBÉ*
Affiliation:
Department of Mathematics, Statistics and Computer Science, Purdue University Northwest, 1401 S. U.S. 421 Westville, IN 46391, USA email atogbe@pnw.edu
*
✉atogbe@pnw.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we consider the Diophantine equations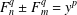

$$\begin{eqnarray}\displaystyle F_{n}^{q}\pm F_{m}^{q}=y^{p} & & \displaystyle \nonumber\end{eqnarray}$$
with positive integers $q,p\geq 2$ and 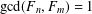$\gcd (F_{n},F_{m})=1$, where $F_{k}$ is a Fibonacci number. We obtain results for 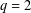$q=2$ or 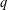$q$ an odd prime with 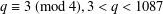$q\equiv 3\;(\text{mod}\;4),3<q<1087$, and complete solutions for 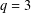$q=3$.

Keywords

exponential equationFibonacci number

MSC classification

Primary: 11D61: Exponential equations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 1 , February 2019 , pp. 34 - 41
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author was supported by NSF of China (No. 11601476) and the Guangdong Provincial Natural Science Foundation (No. 2016A030313013 ) and Foundation for Distinguished Young Teacher in Higher Education of Guangdong, China (YQ2015167). The second author thanks Purdue University Northwest for support.

References

Bennett, M. and Skinner, C., ‘Ternary Diophantine equations via Galois representations and modular forms’, Canad. J. Math. 56 (2004), 23–54.Google Scholar
Bruin, N., ‘On powers as sums of two cubes’, in: Algorithmic Number Theory, Lecture Notes in Computer Science, 1838 (ed. Bosma, W.) (Springer, Berlin, 2000), 169–184.Google Scholar
Bugeaud, Y., Luca, F., Mignotte, M. and Siksek, S., ‘Fibonacci numbers at most one away from a perfect power’, Elem. Math. 63 (2008), 65–75.Google Scholar
Bugeaud, Y., Luca, F., Mignotte, M. and Siksek, S., ‘Almost powers in the Lucas sequence’, J. Théor. Nombres Bordeaux 20 (2008), 555–600.Google Scholar
Bugeaud, Y., Mignotte, M. and Siksek, S., ‘Sur les nombres de Fibonacci de la forme q k y p ’, C. R. Math. Acad. Sci. Paris 339 (2004), 327–330.Google Scholar
Bugeaud, Y., Mignotte, M. and Siksek, S., ‘Classical and modular approaches to exponential Diophantine equations I, Fibonacci and Lucas perfect powers’, Ann. of Math. (2) 163 (2006), 969–1018.Google Scholar
Dahmen, S. R., Classical and Modular Methods Applied to Diophantine Equations, PhD Thesis, University of Utrecht, 2008.Google Scholar
Darmon, H., ‘The equations x n + y n = z 2 and x n + y n = z 3 ’, Int. Math. Res. Not. IMRN 72 (1993), 263–274.Google Scholar
Darmon, H. and Merel, L., ‘Winding quotients and some variants of Fermat’s Last Theorem’, J. reine angew. Math. 490 (1997), 81–100.Google Scholar
Kraus, A., ‘Sur l’équation a 3 + b 3 = c p ’, Exp. Math. 7 (1998), 1–13.Google Scholar
Luca, F. and Patel, V., ‘On perfect powers that are sums of two Fibonacci numbers’, J. Number Theory 189 (2018), 90–96.Google Scholar
McDaniel, W., ‘The g.c.d. in Lucas sequences and Lehmer number sequences’, Fibonacci Quart. 29 (1991), 24–29.Google Scholar
Nagell, T., ‘Løsning til oppgave nr 2’, Nordisk Mat. Tidskr. 30 (1948), 62–64.Google Scholar