Article contents
POROSITY OF CERTAIN SUBSETS OF LEBESGUE SPACES ON LOCALLY COMPACT GROUPS
Published online by Cambridge University Press: 12 December 2012
Abstract
Let 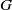 $G$ be a locally compact group. In this paper, we show that if
$G$ be a locally compact group. In this paper, we show that if 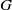 $G$ is a nondiscrete locally compact group,
$G$ is a nondiscrete locally compact group, 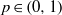 $p\in (0, 1)$ and
$p\in (0, 1)$ and 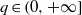 $q\in (0, + \infty ] $, then
$q\in (0, + \infty ] $, then 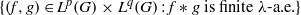 $\{ (f, g)\in {L}^{p} (G)\times {L}^{q} (G): f\ast g\text{ is finite } \lambda \text{-a.e.} \} $ is a set of first category in
$\{ (f, g)\in {L}^{p} (G)\times {L}^{q} (G): f\ast g\text{ is finite } \lambda \text{-a.e.} \} $ is a set of first category in 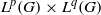 ${L}^{p} (G)\times {L}^{q} (G)$. We also show that if
${L}^{p} (G)\times {L}^{q} (G)$. We also show that if 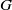 $G$ is a nondiscrete locally compact group and
$G$ is a nondiscrete locally compact group and 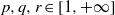 $p, q, r\in [1, + \infty ] $ such that
$p, q, r\in [1, + \infty ] $ such that 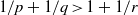 $1/ p+ 1/ q\gt 1+ 1/ r$, then
$1/ p+ 1/ q\gt 1+ 1/ r$, then 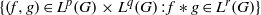 $\{ (f, g)\in {L}^{p} (G)\times {L}^{q} (G): f\ast g\in {L}^{r} (G)\} $, is a set of first category in
$\{ (f, g)\in {L}^{p} (G)\times {L}^{q} (G): f\ast g\in {L}^{r} (G)\} $, is a set of first category in 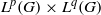 ${L}^{p} (G)\times {L}^{q} (G)$. Consequently, for
${L}^{p} (G)\times {L}^{q} (G)$. Consequently, for 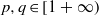 $p, q\in [1+ \infty )$ and
$p, q\in [1+ \infty )$ and 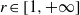 $r\in [1, + \infty ] $ with
$r\in [1, + \infty ] $ with 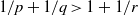 $1/ p+ 1/ q\gt 1+ 1/ r$,
$1/ p+ 1/ q\gt 1+ 1/ r$, 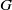 $G$ is discrete if and only if
$G$ is discrete if and only if 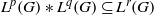 ${L}^{p} (G)\ast {L}^{q} (G)\subseteq {L}^{r} (G)$; this answers a question raised by Saeki [‘The
${L}^{p} (G)\ast {L}^{q} (G)\subseteq {L}^{r} (G)$; this answers a question raised by Saeki [‘The 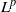 ${L}^{p} $-conjecture and Young’s inequality’, Illinois J. Math. 34 (1990), 615–627].
${L}^{p} $-conjecture and Young’s inequality’, Illinois J. Math. 34 (1990), 615–627].
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright ©2012 Australian Mathematical Publishing Association Inc.
References
- 5
- Cited by


