Hostname: page-component-6bf8c574d5-7jkgd Total loading time: 0 Render date: 2025-02-21T18:07:46.596Z Has data issue: false hasContentIssue false
  • English
  • Français

POSITIVE PROPORTION OF SHORT INTERVALS CONTAINING A PRESCRIBED NUMBER OF PRIMES

Part of: Multiplicative number theory

Published online by Cambridge University Press:  17 May 2019

DANIELE MASTROSTEFANO Open the ORCID record for DANIELE MASTROSTEFANO [Opens in a new window]
DANIELE MASTROSTEFANO*
Affiliation:
University of Warwick, Mathematics Institute, Zeeman Building, Coventry, CV4 7AL, UK email Daniele.Mastrostefano@warwick.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that for every 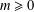$m\geq 0$ there exists an 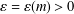$\unicode[STIX]{x1D700}=\unicode[STIX]{x1D700}(m)>0$ such that if 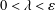$0<\unicode[STIX]{x1D706}<\unicode[STIX]{x1D700}$ and $x$ is sufficiently large in terms of 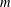$m$ and 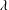$\unicode[STIX]{x1D706}$, then

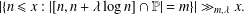$$\begin{eqnarray}|\{n\leq x:|[n,n+\unicode[STIX]{x1D706}\log n]\cap \mathbb{P}|=m\}|\gg _{m,\unicode[STIX]{x1D706}}x.\end{eqnarray}$$
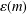The value of $\unicode[STIX]{x1D700}(m)$ and the dependence of the implicit constant on 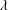$\unicode[STIX]{x1D706}$ and 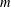$m$ may be made explicit. This is an improvement of the author’s previous result. Moreover, we will show that a careful investigation of the proof, apart from some slight changes, can lead to analogous estimates when allowing the parameters 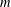$m$ and 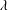$\unicode[STIX]{x1D706}$ to vary as functions of $x$ or replacing the set 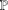$\mathbb{P}$ of all primes by primes belonging to certain specific subsets.

Keywords

primes in short intervalsMaynard’s sieve theory

MSC classification

Primary: 11N05: Distribution of primes
Secondary: 11N36: Applications of sieve methods
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 3 , December 2019 , pp. 378 - 387
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

The author is funded by a Departmental Award and by an EPSRC Doctoral Training Partnership Award.

References

Freiberg, T., ‘Short intervals with a given number of primes’, J. Number Theory 163 (2016), 159–171.Google Scholar
Mastrostefano, D., ‘Short intervals containing a prescribed number of primes’, J. Number Theory 197 (2019), 49–61.Google Scholar
Maynard, J., ‘Dense clusters of primes in subsets’, Compos. Math. 152(7) (2016), 1517–1554.Google Scholar
Murty, M. R. and Murty, V. K., ‘A variant of the Bombieri–Vinogradov theorem’, in: Number Theory (Montreal, Quebec, 1985), CMS Conference Proceedings, 7 (American Mathematical Society, Providence, RI, 1987), 243–272.Google Scholar
Soundararajan, K., ‘The distribution of prime numbers’, in: Equidistribution in Number Theory, An Introduction, NATO Science Series II: Mathematics, Physics and Chemistry, 237 (eds. Granville, A. and Rudnick, Z.) (Springer, Dordrecht, 2007), 59–83.Google Scholar
Thorner, J., ‘Bounded gaps between primes in Chebotarev sets’, Res. Math. Sci. 1(4) (2014), 16 pages.Google Scholar