Article contents
Power integral bases for real cyclotomic fields
Published online by Cambridge University Press: 17 April 2009
Extract
We consider the problem of determining all power integral bases for the maximal real subfield Q (ζ + ζ−1) of the p-th cyclotomic field Q (ζ), where p ≥ 5 is prime and ζ is a primitive p-th root of unity. The ring of integers is Z[ζ+ζ−1] so a power integral basis always exists, and there are further non-obvious generators for the ring. Specifically, we prove that
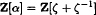 if
if
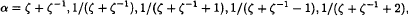 or one of the Galois conjugates of these five algebraic integers. Up to integer translation and multiplication by −1, there are no additional generators for p ≤ 11, and it is plausible that there are no additional generators for p > 13 as well. For p = 13 there is an additional generator, but we show that it does not generalise to an additional generator for 13 < p < 1000.
or one of the Galois conjugates of these five algebraic integers. Up to integer translation and multiplication by −1, there are no additional generators for p ≤ 11, and it is plausible that there are no additional generators for p > 13 as well. For p = 13 there is an additional generator, but we show that it does not generalise to an additional generator for 13 < p < 1000.
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 71 , Issue 1 , February 2005 , pp. 167 - 173
- Copyright
- Copyright © Australian Mathematical Society 2005
References
- 1
- Cited by


