Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T16:42:37.266Z Has data issue: false hasContentIssue false
  • English
  • Français

PROJECTIVE CHARACTERS WITH PRIME POWER DEGREES

Part of: Representation theory of groups

Published online by Cambridge University Press:  28 August 2018

YANG LIU Open the ORCID record for YANG LIU [Opens in a new window]
YANG LIU*
Affiliation:
College of Mathematical Science, Tianjin Normal University, Tianjin 300387, PR China email liuyang@math.pku.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the relationship between structural information of a finite group 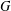$G$ and 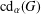$\text{cd}_{\unicode[STIX]{x1D6FC}}(G)$, the set of all irreducible projective character degrees of 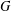$G$ with factor set $\unicode[STIX]{x1D6FC}$. We show that for nontrivial $\unicode[STIX]{x1D6FC}$, if all numbers in 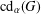$\text{cd}_{\unicode[STIX]{x1D6FC}}(G)$ are prime powers, then 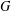$G$ is solvable. Our result is proved by classical character theory using the bijection between irreducible projective representations and irreducible constituents of induced representations in its representation group.

Keywords

finite groupsprojective representationcharacter degrees

MSC classification

Primary: 20C15: Ordinary representations and characters
Secondary: 20C25: Projective representations and multipliers
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 1 , February 2019 , pp. 78 - 82
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The author is supported by NSFC of China (grant no. 11701421) and Introduction of talent research start-up fund of Tianjin Normal University (grant no. 5RL145).

References

Bessenrodt, C. and Olsson, J. B., ‘Prime power degree representations of the double covers of the symmetric and alternating groups’, J. Lond. Math. Soc. 66(2) (2002), 313–324.Google Scholar
Gluck, D. and Wolf, T. R., ‘Brauer’s height conjecture for p-solvable groups’, Trans. Amer. Math. Soc. 282 (1984), 137–152.Google Scholar
Gluck, D. and Wolf, T. R., ‘Defect groups and character heights in blocks of solvable groups. II’, J. Algebra 87 (1984), 222–246.Google Scholar
Guralnick, R., ‘Subgroups of prime power index in a simple group’, J. Algebra 81 (1983), 304–311.Google Scholar
Higgs, R. J., ‘Groups whose projective character degrees are powers of a prime’, Glasg. Math. J. 30(2) (1988), 177–180.Google Scholar
Higgs, R. J., ‘Projective characters of odd degree’, Comm. Algebra 26 (1998), 3133–3140.Google Scholar
Isaacs, I. M., Character Theory of Finite Groups (Academic Press, New York, 1976).Google Scholar
Malle, G. and Zalesskiĭ, A. E., ‘Prime power degree representations of quasi-simple group’, Arch. Math. 77 (2001), 461–468.Google Scholar
Manz, O., ‘Endliche auflösbare Gruppen, deren sämtliche Charaktergrade Primzahlpotenzen sind’ [Finite solvable group all of whose character degrees are prime powers]’, J. Algebra 94(1) (1985), 211–255.Google Scholar
Moretó, A., ‘An answer to a question of Isaacs on character degree graphs’, Adv. Math. 201 (2006), 90–101.Google Scholar
Nagao, H. and Tsushima, Y., Representations of Finite Groups (Academic Press, Boston, 1988).Google Scholar
Navarro, G., ‘Variations on the Itô–Michler theorem on character degrees’, Rocky Mountain J. Math. 46(4) (2016), 1363–1377.Google Scholar
Navarro, G. and Tiep, P. H., ‘Characters of relative p ′ -degree over normal subgroups’, Ann. of Math.(2) 178(3) (2013), 1135–1171.Google Scholar
Navarro, G., Späth, B. and Tiep, P. H., ‘On fully ramified Brauer characters’, Adv. Math. 257 (2014), 248–265.Google Scholar
Willems, W., ‘Blocks of defect zero and degree problems’, in: Proc. Sympos. Pure Math. 47, part I (American Mathematical Society, Providence, RI, 1987), 481–484.Google Scholar