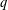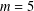Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Guo, Victor J.W.
2020.
Proof of a generalization of the (B.2) supercongruence of Van Hamme through a q-microscope.
Advances in Applied Mathematics,
Vol. 116,
Issue. ,
p.
102016.
Qİ, Feng
CHEN, Chao-ping
and
LIM, Dongkyu
2021.
Several identities containing central binomial coefficients and derived from series expansions of powers of the arcsine function.
Results in Nonlinear Analysis,
Vol. 4,
Issue. 1,
p.
57.
Chen, Jia-Yu
and
Wang, Chen
2022.
Congruences concerning generalized central trinomial coefficients.
Proceedings of the American Mathematical Society,
Vol. 150,
Issue. 9,
p.
3725.
Qi, Feng
Niu, Da-Wei
and
Lim, Dongkyu
2023.
Some combinatorial identities containing central binomial coefficients or Catalan numbers*.
Applied Mathematics in Science and Engineering,
Vol. 31,
Issue. 1,