Hostname: page-component-6bf8c574d5-mggfc Total loading time: 0 Render date: 2025-02-27T18:49:10.158Z Has data issue: false hasContentIssue false
  • English
  • Français

QUADRATIC NONRESIDUES AND NONPRIMITIVE ROOTS SATISFYING A COPRIMALITY CONDITION

Part of: Elementary number theory

Published online by Cambridge University Press:  12 November 2018

JAITRA CHATTOPADHYAY Open the ORCID record for JAITRA CHATTOPADHYAY [Opens in a new window] ,
BIDISHA ROY Open the ORCID record for BIDISHA ROY [Opens in a new window] ,
SUBHA SARKAR Open the ORCID record for SUBHA SARKAR [Opens in a new window]  and
R. THANGADURAI Open the ORCID record for R. THANGADURAI [Opens in a new window]
JAITRA CHATTOPADHYAY
Affiliation:
Harish-Chandra Research Institute, HBNI, Chhatnag Road, Jhunsi, Allahabad-211019, India email jaitrachattopadhyay@hri.res.in
BIDISHA ROY*
Affiliation:
Harish-Chandra Research Institute, HBNI, Chhatnag Road, Jhunsi, Allahabad-211019, India email bidisharoy@hri.res.in
SUBHA SARKAR
Affiliation:
Harish-Chandra Research Institute, HBNI, Chhatnag Road, Jhunsi, Allahabad-211019, India email subhasarkar@hri.res.in
R. THANGADURAI
Affiliation:
Harish-Chandra Research Institute, HBNI, Chhatnag Road, Jhunsi, Allahabad-211019, India email thanga@hri.res.in
*
✉bidisharoy@hri.res.in
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 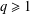$q\geq 1$ be any integer and let 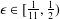$\unicode[STIX]{x1D716}\in [\frac{1}{11},\frac{1}{2})$ be a given real number. We prove that for all primes 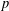$p$ satisfying

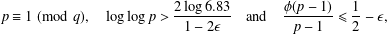$$\begin{eqnarray}p\equiv 1\!\!\!\!\hspace{0.6em}({\rm mod}\hspace{0.2em}q),\quad \log \log p>\frac{2\log 6.83}{1-2\unicode[STIX]{x1D716}}\quad \text{and}\quad \frac{\unicode[STIX]{x1D719}(p-1)}{p-1}\leq \frac{1}{2}-\unicode[STIX]{x1D716},\end{eqnarray}$$
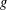there exists a quadratic nonresidue $g$ which is not a primitive root modulo 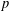$p$ such that 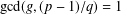$\text{gcd}(g,(p-1)/q)=1$.

Keywords

distribution of nonresiduesprimitive rootsfixed point discrete log problem

MSC classification

Primary: 11A07: Congruences; primitive roots; residue systems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 2 , April 2019 , pp. 177 - 183
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Apostol, T. M., Introduction to Analytic Number Theory, Undergraduate Texts in Mathematics (Springer, New York, 1976).Google Scholar
Gun, S., Luca, F., Rath, P., Sahu, B. and Thangadurai, R., ‘Distribution of residues modulo p ’, Acta Arith. 129(4) (2007), 325–333.Google Scholar
Jarso, T. and Trudgian, T., ‘Quadratic non-residues that are not primitive roots’, Math. Comp., to appear, doi:10.1090/mcom/3378.Google Scholar
Levin, M., Pomerance, C. and Soundararajan, K., ‘Fixed points for discrete logarithms’, in: Algorithmic Number Theory, Lecture Notes in Computer Science, 6197 (Springer, Berlin, 2010), 6–15.Google Scholar
Luca, F., Shparlinski, I. E. and Thangadurai, R., ‘Quadratic non-residue versus primitive roots modulo p ’, J. Ramanujan Math. Soc. 23(1) (2008), 97–104.Google Scholar
Sándor, J., Mitrinović, D. S. and Crstici, B., Handbook on Number Theory I (Springer, Dordrecht, 2001).Google Scholar
Szalay, M., ‘On the distribution of the primitive roots mod p ’, Mat. Lapok 21 (1970), 357–362 (in Hungarian).Google Scholar