Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-02-09T23:02:30.248Z Has data issue: false hasContentIssue false
  • English
  • Français

QUADRILATERAL-TREE PLANAR RAMSEY NUMBERS

Part of: Graph theory

Published online by Cambridge University Press:  30 January 2018

XIAOLAN HU Open the ORCID record for XIAOLAN HU [Opens in a new window] ,
YUNQING ZHANG Open the ORCID record for YUNQING ZHANG [Opens in a new window]  and
YANBO ZHANG Open the ORCID record for YANBO ZHANG [Opens in a new window]
XIAOLAN HU
Affiliation:
School of Mathematics and Statistics, Central China Normal University, Wuhan 430079, PR China email xlhu@mail.ccnu.edu.cn
YUNQING ZHANG*
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, PR China email yunqingzh@nju.edu.cn
YANBO ZHANG
Affiliation:
College of Mathematics and Information Science, Hebei Normal University, Shijiazhuang 050024, PR China email ybzhang@163.com
*
✉yunqingzh@nju.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For two given graphs 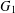$G_{1}$ and 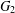$G_{2}$, the planar Ramsey number 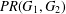$PR(G_{1},G_{2})$ is the smallest integer 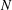$N$ such that every planar graph 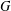$G$ on $N$ vertices either contains 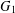$G_{1}$, or its complement contains 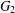$G_{2}$. Let 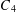$C_{4}$ be a quadrilateral, 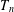$T_{n}$ a tree of order 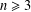$n\geq 3$ with maximum degree 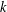$k$, and 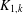$K_{1,k}$ a star of order 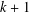$k+1$. We show that 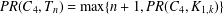$PR(C_{4},T_{n})=\max \{n+1,PR(C_{4},K_{1,k})\}$. Combining this with a result of Chen et al. [‘All quadrilateral-wheel planar Ramsey numbers’, Graphs Combin.33 (2017), 335–346] yields exact values of all the quadrilateral-tree planar Ramsey numbers.

Keywords

quadrilateraltreeplanar Ramsey number

MSC classification

Primary: 05C55: Generalized Ramsey theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 2 , April 2018 , pp. 194 - 199
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author is partially supported by NSFC under grant number 11601176 and NSF of Hubei Province under grant number 2016CFB146; the second author is partially supported by NSFC under grant numbers 11671198 and 11571168; the third author is partially supported by NSFC under grant number 11601527.

References

Burr, S., Erdős, P., Faudree, R. J., Rousseau, C. C. and Schelp, R. H., ‘Some complete bipartite graph-tree Ramsey numbers’, Ann. Discrete Math. 41 (1988), 79–89.CrossRefGoogle Scholar
Chen, Y. J., Miao, Z. K. and Zhou, G. F., ‘All quadrilateral-wheel planar Ramsey numbers’, Graphs Combin. 33 (2017), 335–346.Google Scholar
Grünbaum, B., ‘Grötzsch’s theorem on 3-colorings’, Michigan Math. J. 10 (1963), 303–310.Google Scholar
Hall, P., ‘On representatives of subsets’, J. Lond. Math. Soc. 10 (1935), 26–30.CrossRefGoogle Scholar
Parsons, T. D., ‘Ramsey graphs and block designs I’, Trans. Amer. Math. Soc. 209 (1975), 33–44.Google Scholar
Steinberg, R. and Tovey, C. A., ‘Planar Ramsey numbers’, J. Comb. Theory Ser. B 59 (1993), 288–296.Google Scholar
Walker, K., ‘The analog of Ramsey numbers for planar graphs’, Bull. Lond. Math. 1 (1969), 187–190.Google Scholar
Zhang, X. M., Chen, Y. J. and Cheng, T. C. E., ‘Polarity graphs and Ramsey numbers for C 4 versus stars’, Discrete Math. 340 (2017), 655–660.Google Scholar
Zhang, X. M., Chen, Y. J. and Cheng, T. C. E., ‘Some values of Ramsey numbers for C 4 versus stars’, Finite Fields Appl. 45 (2017), 73–85.CrossRefGoogle Scholar