REGULARITY OF POWERS OF BIPARTITE GRAPHS

Abstract

For a simple bipartite graph G, we give an upper bound for the regularity of powers of the edge ideal 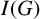$I(G)$ in terms of its vertex domination number. Consequently, we explicitly compute the regularity of powers of the edge ideal of a bipartite Kneser graph. Further, we compute the induced matching number of a bipartite Kneser graph.

1 Introduction

Let $S=\mathsf {k}[x_{1},\ldots ,x_{n}]$ be a polynomial ring, where $\mathsf {k}$ is a field. For a homogeneous ideal I, Cutkosky et al. [5] and independently Kodiyalam [11] proved that $\mathrm {reg}(S/I^{s})=as+b$ for some $a, b \in \mathbb {Z}$ and $s\gg 0.$ The value of a can be determined by the degrees of generators of I but the value of b is quite mysterious. During the last few decades, many researchers have studied the problem of understanding the value of b for some special classes of ideals, for example, edge ideals and cover ideals. In this paper, we consider the edge ideal $I(G)$ of a bipartite graph G and find an upper bound for the value of b in terms of a combinatorial invariant of G.

For any graph G, it is known that

$$ \begin{align*}\nu(G) \leq \mathrm{reg}(S/I(G)) \leq \text{co-chord}(G),\end{align*} $$

where $\nu (G)$ denotes the induced matching number of G and co-chord $(G)$ denotes the co-chordal number of G (see [10, 14]). Bıyıkoğlu and Civan in [4] proved that for any graph G, $\mathrm {reg}(S/I(G) ) \leq \beta (G),$ where $\beta (G)$ is called the upper independent vertex-wise domination set of G (see Definition 2.1(vi)). Beyarslan et al. in [3] proved that for any graph G,

$$ \begin{align*} \mathrm{reg}(S/I(G)^{s}) \geq 2s + \nu(G) - 2 \quad\text{for } s\geq 1.\end{align*} $$

Moreover, they proved that in the special cases of forests (for $s \geq 1$ ) and cycles ( $s \geq 2$ ), the equality holds. In [8], it is shown that for bipartite graphs,

$$ \begin{align*} \mathrm{reg}(S/I(G)^{s}) \leq 2s + \text{co-chord}(G) - 2 \quad\text{for } s\geq 1.\end{align*} $$

Recently, Herzog and Hibi [7] obtained a new upper bound for the regularity of powers of the ideal of a graph G. They proved that

$$ \begin{align*} \mathrm{reg}(S/I(G)^{s}) \leq 2s + c-1 \quad\text{for } s\geq 1,\end{align*} $$

where c is the dimension of the independence complex $\Delta (G)$ of G.

In Section 3, we prove the main result of this paper, which gives a new upper bound for $\mathrm {reg}(S/I(G)^{s} )$ for any bipartite graph G.

Theorem 1.1 (Theorem 3.11).

Let G be a bipartite graph and $I(G)$ be its edge ideal. Then $\mathrm {reg}(S/I(G)^{s+1}) \leq 2s+\beta (G)$ for all $s \geq 0$ .

To prove Theorem 3.11, we use the technique of even-connection with respect to the s-fold product $e_{1} \cdots e_{s}$ of edges (see Definition 2.5), which was introduced by Banerjee in [2]. Alilooee and Banerjee [1] proved that if G is a bipartite graph, then the colon ideal $I(G)^{s+1}:e_{1} \cdots e_{s}$ is a quadratic square-free monomial ideal. Further, the graph $G^{\prime }$ associated to $I(G)^{s+1}:e_{1} \cdots e_{s}$ is also a bipartite graph on the same partition and $G^{\prime }$ is the union of G with all the even-connections with respect to the s-fold product $e_{1} \cdots e_{s}$ (see Remark 3.9).

In Section 4, we study the regularity of powers of edge ideals of the bipartite Kneser graph $\mathcal {H}(m,k)$ for $k \geq 1$ and $m \geq 2k$ (see Definition 2.2). Bipartite Kneser graphs are of great interest because they are Hamiltonian, as shown by Mütze and Su [13]. We are interested in finding the regularity of powers of edge ideals of bipartite Kneser graphs. In [12], it is shown that

$$ \begin{align*}2(s-1)+{2k\choose k}\leq \mathrm{reg}(S/{I(\mathcal{H}(m,k))}^{s})\leq 2(s-1)+{m\choose k},\end{align*} $$

and the lower bound is attained if $m=2k+1$ . It is known that the problem of finding the induced matching number of the graph is an NP-hard problem. Given $k \geq 1$ and $m \geq 2k+1$ , we compute the induced matching number of the bipartite Kneser graph $\mathcal {H}(m,k)$ .

Theorem 1.2 (Corollary 4.3).

For $m\geq 2k+1$ , let $G=\mathcal {H}(m,k)$ be the bipartite Kneser graph. Then the induced matching number of G is given by $\nu (G) = \binom {2k}{k}.$

The following question is posed in [3]: for which graphs G does

$$ \begin{align*}\textrm{reg}(S/I(G)^{s})=2s+\nu(G)-2 \quad\text{for } s \gg 0?\end{align*} $$

For certain classes of graphs, for example, the bipartite $P_{6}$ -free graph and very well-covered, unmixed bipartite, weakly chordal bipartite, forest graphs, it is known that $\textrm {reg}(S/I(G)^{s})=2s+\nu (G)-2$ for $s \gg 0$ (see [3, 8, 9]). Using Theorem 3.11, we prove that the regularity of powers of edge ideals of $\mathcal {H}(m,k)$ attains the lower bound.

Theorem 1.3 (Corollary 4.4).

For $m\geq 2k+1$ , let $G=\mathcal {H}(m,k)$ be the bipartite Kneser graph. Then, for all $s>0$ , $ \mathrm {reg}(S/I(G)^{s} )=2(s-1)+\binom {2k}{k}.$

2 Preliminaries

For a positive integer $n,$ we write $[n]=\{1, 2,\ldots , n\}.$ For a finite set Y, the family of all subsets of Y of size s is denoted by $Y^{(s)}$ .

Definition 2.1. Let G be a simple graph with vertex set $V(G)=\{x_{1},\ldots , x_{n}\}$ and edge set $E(G)$ .

1. (i) For a pair of vertices $x_{i},x_{j}\in V(G)$ , we say $x_{i}$ is adjacent to $x_{j}$ if and only if $x_{i}x_{j}\in E(G).$

2. (ii) A subset W of V is called an independent set if none of the edges of G has both endpoints in W.

3. (iii) For a vertex $v\in V$ , the open neighbourhood of v is $N_{G}(v)=\{x: xv\in E(G)\}$ and the closed neighbourhood of v is $N_{G}[v]=N_{G}(v)\cup \{v\}$ .

4. (iv) For an edge $e=x_{i}x_{j}$ , we define $N_{G}[e]=N_{G}[x_{i}]\cup N_{G}[x_{j}].$

5. (v) An independent set W is called a vertex dominant set if $N_{G}[e]\cap W\neq \varnothing $ for any edge e in G. It is called a minimal vertex dominant set if any proper subset of W is not a vertex-wise dominant set of G.

6. (vi) The upper independent vertex-wise domination number of a graph G is defined by $\beta (G)=\max \{|W|: W\text { is an independent minimal vertex dominating set of } G\}.$

7. (vii) A graph G is called bipartite if $V(G)=X \sqcup Y$ for two independent subsets X and Y of $V(G)$ .

8. (viii) A subgraph $G^{\prime }$ of G is called induced if for every pair of vertices $x_{i}, x_{j}\in V(G^{\prime })$ , $x_{i}x_{j}\in E(G^{\prime })$ if and only if $x_{i}x_{j}\in E(G)$ .

9. (ix) A matching of G is a subgraph of G consisting of pairwise disjoint edges. If the subgraph is an induced subgraph, then the matching is called an induced matching. The largest size of an induced matching in G is called the induced matching number, denoted by $\nu (G).$

10. (x) The graph G is a cycle of length n if after relabelling the vertices of G, the edge set is $E(G)=\{x_{1}x_{2},\ldots , x_{n-1}x_{n},x_{n}x_{1}\}$ .

11. (xi) A finite sequence of vertices $x_{i_{1}},\ldots , x_{i_{r}}$ is called a path from $x_{i_{1}}$ to $x_{i_{r}}$ in G if $x_{i_{j}}x_{i_{j+1}}\in E(G)$ for $1\leq j\leq r-1$ .

12. (xii) A graph is called co-chordal if its complement graph $G^{c}$ does not have any induced cycle of length greater than or equal to $4$ . The co-chordal number, denoted by co-chord $(G)$ , is the minimum number of co-chordal subgraphs required to cover the edges of $G.$

Definition 2.2. The bipartite Kneser graph $\mathcal {H}(m,k)$ is a graph with vertex set $V(G)=[m]^{(k)} \cup [m]^{(m-k)}$ and two distinct vertices $A, B$ are adjacent if and only if $A\subset B$ or $B\subset A. $ For $m= 2k$ , $\mathcal {H}(m,k)$ does not have any edges, so we assume that $m \geq 2k +1.$

Definition 2.3. Let $\mathsf {k}$ be a field and $S=\mathsf {k}[x_{1},x_{2},\ldots ,x_{n}]$ be a standard graded polynomial ring over $\mathsf {k}$ . The Castelnuovo–Mumford regularity of a finitely generated graded S-Module M is given by $\mathrm {reg}(M)=\max _{i,j}\{\kern1.3pt j-i:\mathrm {Tor}_{i}{(M,\mathsf {k})}_{j} \neq 0\}.$

Definition 2.4. Let G be a simple graph with the vertex set $\{x_{1},\ldots ,x_{k}\}$ (without isolated vertices). Then the edge ideal of G is defined as

$$ \begin{align*}I(G)=\langle x_{i}x_{j}: x_{i}x_{j} \text{ is an edge of } G \text{ for some } i,j\rangle.\end{align*} $$

Definition 2.5 [2, Definition 6.2].

Let G be a graph on the vertex set V. Then vertices $x, y\in V$ are called even-connected with respect to the s-fold product $e_{1}\cdots e_{s}$ of edges in G if there exists a path $p_{0}p_{1}\ldots p_{2k+1}$ in G such that:

1. (a) $p_{0}=x$ and $p_{2k+1}=y$ ;

2. (b) $p_{2l+1}p_{2l+2}=e_{i}$ for some i for all l with $0\leq l \leq k-1$ ;

3. (c) $|\{l\geq 0 \mid p_{2l+1}p_{2l+2}=e_{i}\}|\leq |\{\kern1.3pt j \mid e_{j}=e_{i}\}|$ for all i.

Theorem 2.6 [2, Theorem 5.2].

Let G be a simple graph and the set of minimal monomial generators of $I(G)^{s}$ be $\{m_{1},\ldots ,m_{k}\}$ , where $s>0$ . Then,

$$ \begin{align*}\mathrm{reg}( S/I(G)^{s+1} ) \leq \max\{ \mathrm{reg}( S/I(G)^{s+1}:m_{t} )+2s \mbox{ for } 1\leq t \leq k, \mathrm{reg}( S/I(G)^{s}) \}.\end{align*} $$

3 Vertex-wise domination number

In general, there is no relation between $\beta (G)$ and co-chord $(G)$ , for a simple graph G. For example, if $P_{4}$ is a simple path on $4$ vertices, one can check that $\beta (P_{4})=2$ , but $P_{4}$ is a co-chordal graph. However, in [4], it is shown that $\beta (C_{7})=2$ and co-chord $(C_{7})=3$ , where $C_{7}$ denotes the cycle of length $7$ .

Remark 3.1. Let W be a minimal vertex dominant set of G and $w\in W$ . Then there exists an edge $e\in G$ such that $N_{G}[e]\cap W=\{w\}$ .

Notation 3.2. Let G be a triangle-free graph and $I(G)$ its edge ideal. For $x_{1}x_{2} \in E(G)$ , let $G^{\prime }$ be the graph associated to the monomial ideal $I(G)^{2}:x_{1}x_{2}$ . Denote by ${N_{G}(x_{1})\setminus \{x_{2}\}=\{x_{1,1},\ldots , x_{1,r}\}=X_{1}}$ and $N_{G}(x_{2})\setminus \{x_{1}\}=\{x_{2,1},\ldots , x_{2,s}\}=X_{2}.$ To illustrate the notation, we consider a graph G on the vertex set $\{x_{1},x_{2},x_{3},x_{1,1},x_{1,2},x_{2,1},x_{2,2}\}$ and the edge set $E(G)=\{x_{1}x_{2},x_{1}x_{1,1},x_{1}x_{1,2},x_{2}x_{2,1},x_{2}x_{2,2},x_{1,1}x_{3}\}$ , as shown in Figure 1. Then $I(G)^{2}:x_{1}x_{2}=I(G)+\langle x_{1,1}x_{2,1},x_{1,1}x_{2,2},x_{1,2}x_{2,1},x_{1,2}x_{2,2}\rangle $ , that is, $G^{\prime }$ is obtained from the graph G by connecting all vertices of $X_{1}$ with vertices of $X_{2}$ .

Figure 1 Illustrative example for Notation 3.2.

Proposition 3.3. Let G be a triangle-free graph and $I(G)$ be its edge ideal. Let $e \in E(G)$ and $G^{\prime }$ be the graph associated to the monomial ideal $I(G)^{2}:e$ . Then $\beta (G^{\prime })\leq \beta (G)$ .

We prove this proposition in the following sequence of lemmas.

Lemma 3.4. With notation as in Notation 3.2, let W be a minimal vertex dominant set in $G^{\prime }$ such that $W\cap (X_{1}\cup X_{2})=\varnothing $ . Then W is a minimal vertex dominant set in G.

Proof. Since $N_{G}[e]\subset N_{G^{\prime }}[e]\subset N_{G}[e]\cup X_{1}\cup X_{2}$ for any $e\in E(G)$ , we have $N_{G}[e]\cap W=N_{G^{\prime }}[e]\cap W$ . Hence, W is a vertex dominant set in G. We claim that W is a minimal vertex dominant set in G. In contrast, assume that W is not a minimal vertex dominant set in G. Then there exists a vertex $v\in W$ such that $W_{1}=W\setminus \{v\}$ is a vertex dominant set in G. Since W is a minimal vertex dominant set in $G^{\prime }$ , $W_{1}$ is not a vertex dominant set in $G^{\prime }$ . There exists an edge $f\in E(G^{\prime })$ such that $W_{1}\cap N_{G^{\prime }}[f]=\varnothing $ . However, $N_{G}[f]\cap W_{1} = N_{G^{\prime }}[f] \cap W_{1} = \varnothing $ , so $f\notin E(G)$ and hence $f=x_{1,i}x_{2,j}$ for some $i, j$ .

However, note that $v\in N_{G^{\prime }}[f]$ . Since $v\notin X_{1}\cup X_{2}$ , then $v\notin \{x_{1,i},x_{2,j}\}$ and $v\in N_{G}[f].$ Without loss of generality, assume that $vx_{1,i}\in E(G)$ . Since $N_{G}[f]\cap W_{1}=\varnothing $ , we have $N_{G}[x_{1,i}]\cap W_{1}=\varnothing $ and so $N_{G}[v]\cap W_{1}\neq \varnothing $ . This implies that v and some of its adjacent vertices are in W, contradicting the hypothesis that W is an independent set.

Lemma 3.5. With notation as in Notation 3.2, let W be a minimal vertex dominant set in $G^{\prime }$ such that $W\cap X_{1}\neq \varnothing $ . Then $W\cup \{x_{2}\}$ is a vertex dominant set in G.

Proof. First of all, note that since W is an independent set in $G^{\prime }$ and $W\cap X_{1}\neq \varnothing $ , we get $W\cap X_{2}=\varnothing $ . Let f be an edge in G. If $x_{2}\in N_{G}[f]$ , then we are through. Suppose $x_{2}\notin N_{G}[f]$ . This implies that $x_{2,j}$ is not an endpoint of the edge f for any j. Hence, $N_{G}[f]\subset N_{G^{\prime }}[f]\subset N_{G}[f]\cup X_{2}.$ Since $W \cap X_{2}=\varnothing $ , we get $N_{G}[f]\cap W=N_{G^{\prime }}[f]\cap W\neq \varnothing $ , which proves the lemma.

Lemma 3.6. With notation as in Notation 3.2, let W be a minimal vertex dominant set in $G^{\prime }$ such that $W\cap X_{1}\neq \varnothing $ . Let $W_{1}=W\cup \{x_{2}\}.$ Suppose $W_{1}\setminus \{v\}$ is a vertex dominant set in G for some $v\in W_{1}$ . Then $v\in X_{1}\cup \{x_{2}\}$ .

Proof. On the contrary, assume that $v\notin X_{1}\cup \{x_{2}\}$ . Since $W\setminus \{v\}$ is not a vertex dominant set in $G^{\prime }$ , there is an edge $f\in E(G^{\prime })$ such that $N_{G^{\prime }}[f]\cap ( W\setminus \{v\} )=\varnothing $ . If $f= x_{1,i}x_{2,j}$ for some $i, j$ , then $X_{1}\subset N_{G^{\prime }}[f]$ . Hence, $X_{1} \cap ( W\setminus \{v\} ) \subset N_{G^{\prime }}[f]\cap ( W\setminus \{v\} )\neq \varnothing ,$ which is a contradiction to our hypothesis. Therefore, $f\in E(G)$ . Since $N_{G}[f]\subset N_{G^{\prime }}[f]$ and $N_{G^{\prime }}[f]\cap W\setminus \{v\}=\varnothing $ , $N_{G}[f]\cap W\setminus \{v\}=\varnothing $ . Also, we have $N_{G}[f] \cap W_{1} \setminus \{v\} = N_{G}[f] \cap (W \cup \{x_{2}\}) \setminus \{v\} \neq \varnothing .$ Because, $v \neq x_{2},$ we get $ x_{2} \in N_{G}[f]$ . Since $W_{1}\setminus \{v\}$ is a vertex dominant set in $G,$ we get $X_{1}\subset N_{G^{\prime }}[f]$ , reaching the same contradiction.

Lemma 3.7. With notation as in Notation 3.2, let W be a minimal vertex dominant set in $G^{\prime }$ with $W\cap X_{1}\neq \varnothing $ . Let $v\in W\cap X_{1}$ . Then $\widehat {W}=W\setminus \{v\}$ is not a vertex dominant set in G.

Proof. On the contrary, assume that $\widehat {W}=W \setminus \{v\}$ is a vertex dominant set in G. Since $\widehat {W}$ is not a vertex dominant set in $G^{\prime }$ , there exists $f\in E(G^{\prime })$ such that $N_{G^{\prime }}[f]\cap \widehat {W}=\varnothing $ . This implies that $v\in N_{G^{\prime }}[f]$ . Note that $f\notin E(G).$ As for $f\in E(G)$ , we have $N_{G}[f]\cap \widehat {W}\subset N_{G^{\prime }}[f]\cap \widehat {W}=\varnothing $ , which is a contradiction to the fact that $\widehat {W}=W \setminus \{v\}$ is a vertex dominant set of G. Hence, $f=x_{1,i}x_{2,j}$ for some $i,j$ and $N_{G^{\prime }}[f]=N_{G}[x_{1,i}] \cup N_{G}[x_{2,j}] \cup \{X_{1} \cup X_{2}\}.$ This implies that ${N_{G^{\prime }}[f] \cap \widehat {W}=(( N_{G}[x_{1,i}] \cup N_{G}[x_{2,j}] ) \cap \widehat {W}) \cup (\widehat {W}\cap X_{1})\kern1.3pt{=}\kern1.3pt\varnothing.}$ Consider an edge $f^{\prime }=x_{1},x_{1,i} \in E(G).$ Then

(3.1) $$ \begin{align} N_{G}[f^{\prime}]\cap \widehat{W}=(N_{G}[x_{1}] \cup N_{G}[x_{1,i}])\cap \widehat{W}=(\{x_{1}\} \cup X_{1} \cup N_{G}[x_{1,i}])\cap \widehat{W}. \end{align} $$

Note that $x_{1} \notin \widehat {W}$ , because otherwise $N_{G^{\prime }}[f] \cap \widehat {W} \neq \varnothing ,$ which is a contradiction. Since $X_{1} \cap \widehat {W}=\varnothing $ and $N_{G}[x_{1,i}]\cap \widehat {W} \subset ( N_{G}[x_{1,i}] \cup N_{G}[x_{2,j}] ) \cap \widehat {W}=\varnothing ,$ Equation (3.1) gives $N_{G}[f^{\prime }] \cap \widehat {W}=\varnothing ,$ which is a contradiction. Hence, $\widehat {W}=W \setminus \{v\}$ is not a vertex dominant set in G.

Lemma 3.8. With notation as in Notation 3.2, let W be a minimal vertex dominant set in $G^{\prime }$ such that $W \cap X_{1} \neq \varnothing $ and $W_{1}=W \cup \{x_{2}\}$ . Let $\varnothing \neq T \subset W_{1}$ . If $W_{1} \setminus T$ is a vertex dominant set in G, then $|T|\leq 1$ .

Proof. On the contrary, suppose that $|T|\geq 2$ . First we show that $x_{2}\notin T$ . Using Lemma 3.7, we can see that if $x_{2}\in T$ , then $W_{1} \setminus T=W \setminus (T \setminus \{x_{2}\})$ is not a vertex dominant set in G. Thus, $x_{2}\notin T$ .

Let $y \in T \subset W.$ Since W is a minimal vertex dominant set of $G^{\prime }$ , there exists an edge $f \in E(G^{\prime })$ such that $N_{G^{\prime }}[f] \cap W=\{y\}.$ Therefore, $N_{G^{\prime }}[f]\cap (W \setminus T)=\varnothing .$ If $f \in E(G),$ then $\varnothing \neq N_{G}[f] \cap ( W_{1} \setminus T) \subset (N_{G^{\prime }}[f] \cap (W \setminus T)) \cup (N_{G}[f] \cap \{x_{2}\}).$ This implies that $(N_{G}[f] \cap \{x_{2}\}) \neq \varnothing $ , and hence $x_{2} \in N_{G}[f],$ which means that $X_{1} \subset N_{G^{\prime }}[f].$ Thus, ${W\kern-1pt \cap\kern-1pt X_{1}\kern-1pt \subset\kern-1pt N_{G^{\prime }}[f]\kern-1pt \cap\kern-1pt W=\{y\}.}$ Since $W \cap X_{1} \neq \varnothing ,$ we have $W\kern-1pt \cap\kern-1pt X_{1}=\{y\}$ . Let $y^{\prime } \in T\setminus \{y\}$ . Then $y^{\prime } \notin X_{1}.$ Now the fact that $W_{1} \setminus T$ is a vertex dominant set in G implies that $W_{1} \setminus \{y^{\prime }\}$ is a vertex dominant set in $G,$ which gives a contradiction to Lemma 3.6. If $f \in E(G^{\prime })\setminus E(G)$ , then $X_{1} \subset N_{G^{\prime }}[f].$ Now proceeding as before, $W_{1}\setminus \{ v\}$ is a vertex dominant set in G for some $v \notin X_{1} \cap \{x_{2}\}$ , which is a contradiction by Lemma 3.6.

Proof of Proposition 3.3.

Let W be a minimal vertex dominating set of $G^{\prime }$ . If we have $W \cap \{X_{1} \cup X_{2}\} =\varnothing $ , then by Lemma 3.4, W is a minimal vertex dominating set of G. Otherwise, using Lemma 3.5, $W_{1}=W \cup \{x_{2}\}$ is a vertex dominating set of G. Further, by Lemma 3.8, either $W_{1}=W \cup \{x_{2}\}$ is a minimal vertex dominating set of G or $W_{1} \setminus \{v\}$ is a minimal vertex dominating set of G for some $v \in W_{1}.$ It follows from the definition of $\beta (G)$ that $\beta (G^{\prime })\leq \beta (G).$

To prove our main theorem, we shall use the following remark.

Remark 3.9. Let G be a bipartite graph and $s \geq 1$ be an integer. Then for every s-fold product $e_{1} \cdots e_{s}, $ the following statements hold.

1. (a) The ideal $(I(G)^{s+1} : e_{1} \cdots e_{s})$ is a quadratic square-free monomial ideal. Moreover, the graph $G^{\prime }$ associated to $(I(G)^{s+1} : e_{1} \cdots e_{s})$ is bipartite on the same vertex set and the same bipartition as G (see [1, Proposition 3.5]).

2. (b) The ideal $I(G)^{s+1}:e_{1}\cdots e_{s}=(I(G)^{2}:e_{1})^{s}:e_{2}\cdots e_{s}$ (see [1, Lemma 3.7]).

Note that if G is a triangle-free graph, then the graph H associated to $I(G)^{2}:e$ need not be a triangle-free graph, for $e \in E(G)$ . Thus, in view of Remark 3.9(a), we prove the following result for bipartite graphs.

Corollary 3.10. Let G be a bipartite graph and u be a minimal monomial generator of $I(G)^{s}$ . Then $\beta (G^{\prime }) \leq \beta (G),$ where $G^{\prime }$ is the graph associated to $I(G)^{s+1}:u$ .

Proof. We use induction on s. For $s=1$ , the result follows from Proposition 3.3. Assume that $s>1$ . Let $u=e_{1}\cdots e_{s}$ for some edges $e_{1}, \ldots , e_{s}$ in the edge set $E(G)$ . If H is the graph associated to $I(G)^{2}:e_{1}$ , then by Proposition 3.3, $\beta (H)\leq \beta (G).$ By Remark 3.9, the graph H is a bipartite graph and $I(G)^{s+1}:e_{1}\cdots e_{s}=I(H)^{s}:e_{2}\cdots e_{s}$ . Hence, by induction, we get $\beta (G^{\prime })\leq \beta (H)\leq \beta (G)$ .

Now we are ready to prove our main theorem.

Theorem 3.11. Let G be a bipartite graph and $I(G)$ be its edge ideal. Then $\mathrm {reg}(S/I(G)^{s+1} ) \leq 2s+\beta (G)$ for all $s \geq 0$ .

Proof. We use induction on s. For $s=0$ , the result follows from [4, Theorem 3.19]. Now assume that $s\ge 1$ . In view of Theorem 2.6, it is enough to prove that

$$ \begin{align*}\mathrm{reg} ( {S}/{I(G)^{s+1}:u}) \leq \beta(G)\end{align*} $$

for all minimal monomial generators u of $I(G)^{s}$ . Let $G^{\prime }$ be the graph associated to $(I(G)^{s+1} : u)$ . Now, the proof follows from Corollary 3.10 and [4, Theorem 3.19].

4 Bipartite Kneser graphs

Theorem 4.1 (Frankl, [6]).

Suppose $\mathcal {A}=\{A_{1},\ldots , A_{l}\}$ is a family of r-sets and $\mathcal {B}=\{B_{1},\ldots , B_{l}\}$ is a family of s-sets such that:

1. (i) $A_{i} \cap B_{i}=\varnothing $ for $1 \leq i \leq m$ ;

2. (ii) $A_{i} \cap B_{j} \neq \varnothing $ for $1 \leq i<j\leq m.$

Then

$$ \begin{align*}l \leq \binom{r+s}{s}.\end{align*} $$

Proposition 4.2. Let $G=\mathcal {H}(m,k)$ be the bipartite Kneser graph. Then $\beta (G) \leq \binom {2k}{k}.$

Proof. Let $W=\{C_{1},\ldots ,C_{t},C_{t+1},\ldots ,C_{m}\}$ be a minimal vertex dominant set in G, where $C_{i} \in [n]^{(k)}, 1 \leq i \leq t$ , and $C_{i} \in [n]^{(n-k)}, t+1 \leq i \leq m.$ Since W is a minimal vertex dominant set in G, for each vertex $C_{i} \in W$ , there exists a vertex $D_{i}$ such that $N_{G}(D_{i})\cap W=\{C_{i}\}$ . This implies that

$$ \begin{align*} C_{i} \subset D_{j} &\quad \text{if and only if } i=j,\quad 1\leq i,j \leq t \\ C_{j} \supset D_{i} &\quad \text{if and only if } i=j,\quad t+1\leq i,j \leq m. \end{align*} $$

Therefore,

$$ \begin{align*} C_{i} \cap D_{j}^{c}=\phi &\quad \text{if and only if } i=j,\quad 1\leq i,j \leq t \\ C_{j}^{c}\cap D_{i}=\phi &\quad \text{if and only if } i=j,\quad t+1\leq i,j \leq m. \end{align*} $$

Consider the collection $W^{\prime }=\{(X_{1},Y_{1}),\ldots ,(X_{m},Y_{m})\}$ of ordered pairs, where $X_{i}=C_{i},Y_{i}=D_{i}^{c}$ for $1\leq i \leq t$ and $X_{i}=D_{i},Y_{i}=C_{i}^{c}$ for $ t+1\leq i \leq m$ . By the choice of the collection $W^{\prime }$ , it is clear that $X_{i}\cap Y_{i}=\varnothing $ for all i, and $X_{i}\cap Y_{j}\neq \varnothing $ for $1\leq i<j\leq t$ and $t+1\leq i<j\leq m$ . Now, since W is an independent set, $C_{i}\not \subset C_{j}$ and hence $C_{i}\cap C_{j}^{c}\neq \varnothing $ for all $i\neq j$ . Therefore, $X_{i}\cap Y_{j}\neq \varnothing $ for $1\leq i\leq t$ and $t+1\leq j\leq m$ . This implies that $X_{i}\cap Y_{j}\neq \varnothing $ for $1\leq i<j\leq m$ and $X_{i}\cap Y_{i}= \varnothing $ for $1\leq i\leq m.$ Since $|X_{i}|=|Y_{i}|=k$ for all i, in view of Theorem 4.1, we get $m \leq \binom {2k}{k}$ .

Corollary 4.3. For $m\geq 2k+1$ , let $G=\mathcal {H}(m,k)$ be the bipartite Kneser graph. Then the induced matching number of G is given by $\nu (G) = \binom {2k}{k}.$

Proof. In view of [10, Lemma 2.2] and [4, Theorem 3.19],

$$ \begin{align*}\nu(G) \leq \mathrm{reg}(S/I(G) ) \leq \beta(G).\end{align*} $$

Using [12, Lemma 4.2], $\nu (G) \geq \binom {2k}{k}$ . Now, by Proposition 4.2, $\nu (G)=\binom {2k}{k}.$

Corollary 4.4. For $m\geq 2k+1$ , let $G=\mathcal {H}(m,k)$ be the bipartite Kneser graph. Then, for all $s>0$ , $ \mathrm {reg}(S/I(G)^{s} )=2(s-1)+\binom {2k}{k}.$

Proof. From [3, Theorem 4.5] and Corollary 4.3, $ \mathrm {reg}(S/I(G)^{s} ) \geq 2(s-1)+\binom {2k}{k}.$ Now, by Theorem 3.11 and Proposition 4.2, $ \mathrm {reg}(S/I(G)^{s} ) \leq 2(s-1)+\binom {2k}{k},$ and hence we get the desired result.