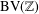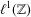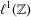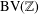Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Carneiro, Emanuel
Madrid, José
and
Pierce, Lillian B.
2017.
Endpoint Sobolev and BV continuity for maximal operators.
Journal of Functional Analysis,
Vol. 273,
Issue. 10,
p.
3262.
Liu, Feng
and
Xu, Lei
2018.
A Note on the Regularity of the Two-Dimensional One-Sided Hardy-Littlewood Maximal Function.
Journal of Function Spaces,
Vol. 2018,
Issue. ,
p.
1.
Liu, Feng
and
Xu, Lei
2018.
Regularity of one-sided multilinear fractional maximal functions.
Open Mathematics,
Vol. 16,
Issue. 1,
p.
1556.
Liu, Feng
2018.
On the regularity of one-sided fractional maximal functions.
Mathematica Slovaca,
Vol. 68,
Issue. 5,
p.
1097.
Liu, Feng
2018.
Endpoint regularity of discrete multisublinear fractional maximal operators associated with
ℓ
1
$\ell^{1}$
-balls.
Journal of Inequalities and Applications,
Vol. 2018,
Issue. 1,
Zhang, Daiqing
2019.
Endpoint regularity of discrete multilinear fractional nontangential maximal functions.
Advances in Difference Equations,
Vol. 2019,
Issue. 1,
Yang, Yu-Guang
Li, Bo-Ran
Kang, Shuang-Yong
Chen, Xiu-Bo
Zhou, Yi-Hua
and
Shi, Wei-Min
2019.
New quantum key agreement protocols based on cluster states.
Quantum Information Processing,
Vol. 18,
Issue. 3,
Yang, Yu-Guang
Gao, Shang
Li, Dan
Zhou, Yi-Hua
and
Shi, Wei-Min
2019.
Two-party quantum key agreement over a collective noisy channel.
Quantum Information Processing,
Vol. 18,
Issue. 3,
Yang, Yu-Guang
Cao, Sheng-Nan
Cao, Wei-Feng
Li, Dan
Zhou, Yi-Hua
and
Shi, Wei-Min
2019.
Generalized teleportation by means of discrete-time quantum walks on N-lines and N-cycles.
Modern Physics Letters B,
Vol. 33,
Issue. 06,
p.
1950070.
Cao, Wei-Feng
and
Yang, Yu-Guang
2019.
Verifiable Quantum Secret Sharing Protocols Based on Four-Qubit Entangled States.
International Journal of Theoretical Physics,
Vol. 58,
Issue. 4,
p.
1202.
Zhang, Daiqing
2020.
Regularity of Commutators of the One-Sided Hardy-Littlewood Maximal Functions.
Journal of Function Spaces,
Vol. 2020,
Issue. ,
p.
1.
Liu, Feng
and
Zhang, Xiao
2021.
Sobolev Regularity of Maximal Operators on Infinite Connected Graphs.
Mediterranean Journal of Mathematics,
Vol. 18,
Issue. 3,
Zhang, Xiao
2021.
Endpoint Regularity of the Discrete Multisublinear Fractional Maximal Operators.
Results in Mathematics,
Vol. 76,
Issue. 2,
Garbaliauskienė, Virginija
Macaitienė, Renata
and
Šiaučiūnas, Darius
2023.
ON THE FUNCTIONAL INDEPENDENCE OF THE RIEMANN ZETA-FUNCTION.
Mathematical Modelling and Analysis,
Vol. 28,
Issue. 2,
p.
352.
Daiqing, Zhang
and
Feng, Liu
2024.
Endpoint regularity for discrete multilinear maximal operators and their fractional variants.
SCIENTIA SINICA Mathematica,