No CrossRef data available.
Article contents
REPRESENTATION FUNCTIONS ON ABELIAN GROUPS
Published online by Cambridge University Press: 15 August 2018
Abstract
Let 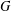 $G$ be a finite abelian group,
$G$ be a finite abelian group, 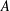 $A$ a nonempty subset of
$A$ a nonempty subset of 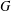 $G$ and
$G$ and 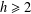 $h\geq 2$ an integer. For
$h\geq 2$ an integer. For 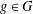 $g\in G$, let
$g\in G$, let 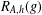 $R_{A,h}(g)$ denote the number of solutions of the equation
$R_{A,h}(g)$ denote the number of solutions of the equation 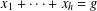 $x_{1}+\cdots +x_{h}=g$ with
$x_{1}+\cdots +x_{h}=g$ with 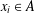 $x_{i}\in A$ for
$x_{i}\in A$ for 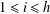 $1\leq i\leq h$. Kiss et al. [‘Groups, partitions and representation functions’, Publ. Math. Debrecen85(3) (2014), 425–433] proved that (a) if
$1\leq i\leq h$. Kiss et al. [‘Groups, partitions and representation functions’, Publ. Math. Debrecen85(3) (2014), 425–433] proved that (a) if 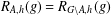 $R_{A,h}(g)=R_{G\setminus A,h}(g)$ for all
$R_{A,h}(g)=R_{G\setminus A,h}(g)$ for all 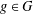 $g\in G$, then
$g\in G$, then 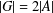 $|G|=2|A|$, and (b) if
$|G|=2|A|$, and (b) if 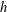 $h$ is even and
$h$ is even and 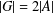 $|G|=2|A|$, then
$|G|=2|A|$, then 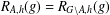 $R_{A,h}(g)=R_{G\setminus A,h}(g)$ for all
$R_{A,h}(g)=R_{G\setminus A,h}(g)$ for all 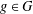 $g\in G$. We prove that
$g\in G$. We prove that 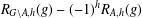 $R_{G\setminus A,h}(g)-(-1)^{h}R_{A,h}(g)$ does not depend on
$R_{G\setminus A,h}(g)-(-1)^{h}R_{A,h}(g)$ does not depend on 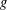 $g$. In particular, if
$g$. In particular, if 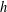 $h$ is even and
$h$ is even and 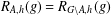 $R_{A,h}(g)=R_{G\setminus A,h}(g)$ for some
$R_{A,h}(g)=R_{G\setminus A,h}(g)$ for some 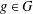 $g\in G$, then
$g\in G$, then 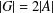 $|G|=2|A|$. If
$|G|=2|A|$. If 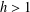 $h>1$ is odd and
$h>1$ is odd and 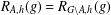 $R_{A,h}(g)=R_{G\setminus A,h}(g)$ for all
$R_{A,h}(g)=R_{G\setminus A,h}(g)$ for all 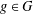 $g\in G$, then
$g\in G$, then 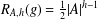 $R_{A,h}(g)=\frac{1}{2}|A|^{h-1}$ for all
$R_{A,h}(g)=\frac{1}{2}|A|^{h-1}$ for all 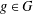 $g\in G$. If
$g\in G$. If 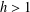 $h>1$ is odd and
$h>1$ is odd and 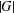 $|G|$ is even, then there exists a subset
$|G|$ is even, then there exists a subset 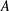 $A$ of
$A$ of 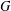 $G$ with
$G$ with 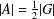 $|A|=\frac{1}{2}|G|$ such that
$|A|=\frac{1}{2}|G|$ such that 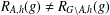 $R_{A,h}(g)\not =R_{G\setminus A,h}(g)$ for all
$R_{A,h}(g)\not =R_{G\setminus A,h}(g)$ for all 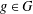 $g\in G$.
$g\in G$.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2018 Australian Mathematical Publishing Association Inc.
Footnotes
This work was supported by the National Natural Science Foundation of China, No. 11771211.

