Article contents
THE RESTRICTED ISOMETRY PROPERTY FOR SIGNAL RECOVERY WITH COHERENT TIGHT FRAMES
Published online by Cambridge University Press: 19 August 2015
Abstract
In this paper, we consider signal recovery via 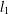 $l_{1}$-analysis optimisation. The signals we consider are not sparse in an orthonormal basis or incoherent dictionary, but sparse or nearly sparse in terms of some tight frame
$l_{1}$-analysis optimisation. The signals we consider are not sparse in an orthonormal basis or incoherent dictionary, but sparse or nearly sparse in terms of some tight frame 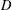 $D$. The analysis in this paper is based on the restricted isometry property adapted to a tight frame
$D$. The analysis in this paper is based on the restricted isometry property adapted to a tight frame 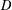 $D$ (abbreviated as
$D$ (abbreviated as 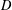 $D$-RIP), which is a natural extension of the standard restricted isometry property. Assuming that the measurement matrix
$D$-RIP), which is a natural extension of the standard restricted isometry property. Assuming that the measurement matrix 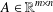 $A\in \mathbb{R}^{m\times n}$ satisfies
$A\in \mathbb{R}^{m\times n}$ satisfies 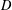 $D$-RIP with constant
$D$-RIP with constant 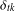 ${\it\delta}_{tk}$ for integer
${\it\delta}_{tk}$ for integer 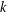 $k$ and
$k$ and 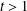 $t>1$, we show that the condition
$t>1$, we show that the condition 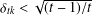 ${\it\delta}_{tk}<\sqrt{(t-1)/t}$ guarantees stable recovery of signals through
${\it\delta}_{tk}<\sqrt{(t-1)/t}$ guarantees stable recovery of signals through 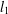 $l_{1}$-analysis. This condition is sharp in the sense explained in the paper. The results improve those of Li and Lin [‘Compressed sensing with coherent tight frames via
$l_{1}$-analysis. This condition is sharp in the sense explained in the paper. The results improve those of Li and Lin [‘Compressed sensing with coherent tight frames via 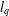 $l_{q}$-minimization for
$l_{q}$-minimization for 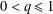 $0<q\leq 1$’, Preprint, 2011, arXiv:1105.3299] and Baker [‘A note on sparsification by frames’, Preprint, 2013, arXiv:1308.5249].
$0<q\leq 1$’, Preprint, 2011, arXiv:1105.3299] and Baker [‘A note on sparsification by frames’, Preprint, 2013, arXiv:1308.5249].
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 92 , Issue 3 , December 2015 , pp. 496 - 507
- Copyright
- © 2015 Australian Mathematical Publishing Association Inc.
References
- 2
- Cited by

