Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Aghajani, A.
and
Jalilian, Y.
2010.
Existence and global attractivity of solutions of a nonlinear functional integral equation.
Communications in Nonlinear Science and Numerical Simulation,
Vol. 15,
Issue. 11,
p.
3306.
Ben Amar, Afif
2015.
On an integral equation under Henstock–Kurzweil–Pettis integrability.
Arabian Journal of Mathematics,
Vol. 4,
Issue. 2,
p.
91.
Li, Baolin
and
Gou, Haide
2016.
On the Existence of Weak Solutions of Nonlinear Integral Equations in Banach Spaces.
Mediterranean Journal of Mathematics,
Vol. 13,
Issue. 5,
p.
2633.
Li, Baolin
and
Gou, Haide
2016.
Weak solutions nonlinear fractional integrodifferential equations in nonreflexive Banach spaces.
Boundary Value Problems,
Vol. 2016,
Issue. 1,
Habani, Sadek
and
Seba, Djamila
2022.
Proceedings of the International Conference on Fractional Differentiation and its Applications (ICFDA’21).
Vol. 452,
Issue. ,
p.
208.
Sikorska-Nowak, Aneta
2023.
Integrodifferential equations of mixed type on time scales with Delta-HK and Delta-HKP integrals.
Electronic Journal of Differential Equations,
Vol. 2023,
Issue. 01-37,
p.
29.

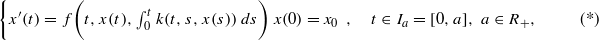
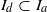 .
.