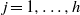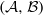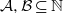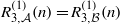Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
QU, ZHENHUA
2015.
ON A PARTITION PROBLEM OF FINITE ABELIAN GROUPS.
Bulletin of the Australian Mathematical Society,
Vol. 92,
Issue. 1,
p.
24.
Rozgonyi, Eszter
and
Sándor, Csaba
2017.
An extension of Nathanson’s Theorem on representation functions.
Combinatorica,
Vol. 37,
Issue. 3,
p.
521.