Article contents
THE SHARP BOUND OF THE SECOND HANKEL DETERMINANT OF LOGARITHMIC COEFFICIENTS FOR STARLIKE AND CONVEX FUNCTIONS
Published online by Cambridge University Press: 06 November 2024
Abstract
Let 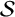 $\mathcal {S}$ denote the class of univalent functions in the open unit disc
$\mathcal {S}$ denote the class of univalent functions in the open unit disc 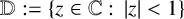 $\mathbb {D}:=\{z\in \mathbb {C}:\, |z|<1\}$ with the form
$\mathbb {D}:=\{z\in \mathbb {C}:\, |z|<1\}$ with the form 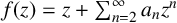 $f(z)= z+\sum _{n=2}^{\infty }a_n z^n$. The logarithmic coefficients
$f(z)= z+\sum _{n=2}^{\infty }a_n z^n$. The logarithmic coefficients 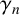 $\gamma _{n}$ of
$\gamma _{n}$ of 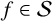 $f\in \mathcal {S}$ are defined by
$f\in \mathcal {S}$ are defined by 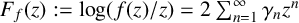 $F_{f}(z):= \log (f(z)/z)=2\sum _{n=1}^{\infty }\gamma _{n}z^{n}$. The second Hankel determinant for logarithmic coefficients is defined by
$F_{f}(z):= \log (f(z)/z)=2\sum _{n=1}^{\infty }\gamma _{n}z^{n}$. The second Hankel determinant for logarithmic coefficients is defined by 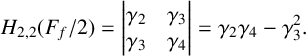 $$ \begin{align*} H_{2,2}(F_f/2) = \begin{vmatrix} \gamma_2 & \gamma_3 \\ \gamma_3 & \gamma_4 \end{vmatrix} =\gamma_2\gamma_4 -\gamma_3^2. \end{align*} $$
$$ \begin{align*} H_{2,2}(F_f/2) = \begin{vmatrix} \gamma_2 & \gamma_3 \\ \gamma_3 & \gamma_4 \end{vmatrix} =\gamma_2\gamma_4 -\gamma_3^2. \end{align*} $$
We obtain sharp upper bounds of the second Hankel determinant of logarithmic coefficients for starlike and convex functions.
Keywords
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 112 , Issue 1 , August 2025 , pp. 163 - 171
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The research of the second author is supported by UGC-JRF.
References
- 1
- Cited by


