Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
CHAN, HENG HUAT
and
COOPER, SHAUN
2012.
Rational analogues of Ramanujan's series for 1/π.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 153,
Issue. 2,
p.
361.
Morton, Patrick
2014.
Supersingular parameters of the Deuring normal form.
The Ramanujan Journal,
Vol. 33,
Issue. 3,
p.
339.
Cooper, Shaun
2017.
Ramanujan's Theta Functions.
p.
509.
Cooper, Shaun
2017.
Ramanujan's Theta Functions.
p.
467.
Cooper, Shaun
2017.
Ramanujan's Theta Functions.
p.
613.
Aygin, Zafer Selcuk
and
Toh, Pee Choon
2019.
When is the derivative of an eta quotient another eta quotient?.
Journal of Mathematical Analysis and Applications,
Vol. 480,
Issue. 1,
p.
123366.
Choi, Dohoon
Kim, Byungchan
and
Lim, Subong
2019.
Pairs of eta-quotients with dual weights and their applications.
Advances in Mathematics,
Vol. 355,
Issue. ,
p.
106779.
Cooper, Shaun
Huber, Timothy
and
Opoku, Jeffery
2025.
Ramanujan–Fine integrals for level 10.
The Ramanujan Journal,
Vol. 66,
Issue. 2,


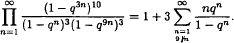 The proof uses only a few well-known properties of the cubic theta functions
The proof uses only a few well-known properties of the cubic theta functions 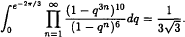 .
.