Article contents
Slice convergence of parametrised sums of convex functions in non-reflexive spaces
Published online by Cambridge University Press: 17 April 2009
Extract
The objectives of this study of slice convergence are two-fold. The first is to derive results regarding the passage of certain semi–convergences through Young–Fenchel conjugation. These semi–convergences arise from the splitting of the usual slice topology in the primal and dual spaces into (non-Hausdorff) topologies: the upper slice topology 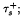 ; a topology
; a topology 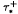 generating a convergence closely resembling the bounded–weak* upper Kuratowski convergence; along with the respective primal and dual lower Kuratowski topologies. This gives rise to topological convergences not reliant on sequentially–based definitions found in many such studies, and associated topological continuity results for conjugation (in normed spaces), in contrast to the usual sequential continuity exhibited by analogues of Mosco convergence. The second objective is to study the passage of slice convergence through addition. Such sum theorems have been derived in other works and we establish previous theorems from a unified framework as well as obtaining a new result.
generating a convergence closely resembling the bounded–weak* upper Kuratowski convergence; along with the respective primal and dual lower Kuratowski topologies. This gives rise to topological convergences not reliant on sequentially–based definitions found in many such studies, and associated topological continuity results for conjugation (in normed spaces), in contrast to the usual sequential continuity exhibited by analogues of Mosco convergence. The second objective is to study the passage of slice convergence through addition. Such sum theorems have been derived in other works and we establish previous theorems from a unified framework as well as obtaining a new result.
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 60 , Issue 3 , December 1999 , pp. 429 - 458
- Copyright
- Copyright © Australian Mathematical Society 1999
References
- 6
- Cited by


