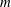Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shao, Changguo
and
Jiang, Qinhui
2018.
Structure of finite groups with four conjugacy class sizes of certain elements.
Communications in Algebra,
Vol. 46,
Issue. 4,
p.
1484.
Jiang, Qinhui
Shao, Changguo
and
Zhao, Yan
2020.
Finite groups with exactly one composite conjugacy class size.
Proceedings - Mathematical Sciences,
Vol. 130,
Issue. 1,
Shao, Changguo
and
Jiang, Qinhui
2020.
Determining group structure by set of conjugacy class sizes.
Communications in Algebra,
Vol. 48,
Issue. 4,
p.
1626.