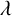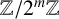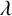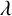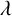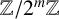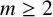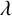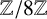SOME COUNTING FORMULAE FOR $\lambda $-QUIDDITIES OVER THE RINGS ${\mathbb {Z}}/2^{m}{\mathbb {Z}}$

Abstract

The $\lambda $-quiddities of size n are n-tuples of elements of a fixed set, solutions of a matrix equation appearing in the study of Coxeter’s friezes. Their number and properties are closely linked to the structure and the cardinality of the chosen set. Our main objective is an explicit formula giving the number of $\lambda $-quiddities of odd size, and a lower and upper bound for the number of $\lambda $-quiddities of even size, over the rings ${\mathbb {Z}}/2^{m}{\mathbb {Z}}$ ($m \geq 2$). We also give explicit formulae for the number of $\lambda $-quiddities of size n over ${\mathbb {Z}}/8{\mathbb {Z}}$.

1. Introduction

Coxeter’s friezes are mathematical objects which are closely linked to many topics (see for example [8]). They were introduced at the beginning of the 1970s by Coxeter (see [2]) and are defined as tables of numbers, belonging to a fixed set, having a finite number of lines of infinite length, arranged with an offset, and for which some arithmetic relations are verified. One of the main elements of the study of Coxeter’s friezes is the resolution of the following equation over the chosen set:

$$ \begin{align*}M_{n}(a_1,\ldots,a_n):=\begin{pmatrix} a_{n} & -1 \\[4pt] 1 & 0 \end{pmatrix} \begin{pmatrix} a_{n-1} & -1 \\[4pt] 1 & 0 \end{pmatrix} \cdots \begin{pmatrix} a_{1} & -1 \\[4pt] 1 & 0 \end{pmatrix}=-{\mathrm{Id}}.\end{align*} $$

In particular, the intervention of the matrices $M_{n}(a_1,\ldots ,a_n)$ is very interesting since they are involved in the study of many other mathematical objects, such as ‘negative’ continued fractions and discrete Sturm–Liouville equations.

The study of the previous equation naturally leads to the generalised equation

(E _R ) $$\begin{align}M_{n}(a_1,\ldots,a_n)=\pm \mathrm{Id} \end{align}$$

over a subset R of a commutative and unitary ring A. We will say that a solution $(a_1,\ldots ,a_n)$ of ( E _R ) is a $\lambda $ -quiddity of size n over R (if there is no ambiguity, we will omit the set over which we are working) and our goal is to study these objects over different sets. There are several ways to achieve this objective. For example, we can try to find a recursive construction and a combinatorial description of the solutions. In this way, we have precise results about the solutions of $(E_{\mathbb {N}^{*}})$ (see [10]). We can also define a notion of irreducible solutions and study them (see for example [3, 5, 6]). We can also, and this is what we will do here, look for general information, such as the number of solutions of fixed size. In this direction, we already have formulae for $R=\mathbb {N}^{*}$ (see [1]) and for $R=\mathbb {F}_{q}$ . We recall the results in this case. For q the power of a prime number p, $B \in {\mathrm {SL}}_{2}(\mathbb {F}_{q})$ and $n \in \mathbb {N}^{*}$ ,

$$ \begin{align*} u_{n,q}^{+} & :=|\{(a_{1},\ldots,a_{n})\in\mathbb{F}_{q}^{n},~M_{n}(a_{1},\ldots,a_{n})={\mathrm{Id}}\}| \\ u_{n,q}^{-} & :=|\{(a_{1},\ldots,a_{n})\in\mathbb{F}_{q}^{n},~M_{n}(a_{1},\ldots,a_{n})=-{\mathrm{Id}}\}|. \end{align*} $$

Moreover, if $m \in {\mathbb {N^{*}}}$ and $k \geq 2$ ,

$$ \begin{align*}[m]_{k}:=\frac{k^{m}-1 }{k-1} \quad\mbox{and}\quad \binom{m}{2}_{k}:=\frac{(k^{m}-1)(k^{m-1}-1)}{(k-1)(k^{2}-1)}.\end{align*} $$

Theorem 1.1 (Morier-Genoud, [9, Theorem 1]).

Let q be the power of a prime number p and $b\in\mathbb{N}$ , $n>4$ .

1. (i) If n is odd, then $u_{n,q}^{-}=[\tfrac{n-1}{2}]_{q^2}$ .

2. (ii) If n is even, then there exists $m \in {\mathbb {N^{*}}}$ such that $n=2m$ .

   1. (a) If $p=2$ , $u_{n,q}^{-}=(q-1)\binom {m}{2}_{q}+q^{m-1}$ .

   2. (b) If $p>2$ and m is even, $u_{n,q}^{-}=(q-1)\binom {m}{2}_{q}$ .

   3. (c) If $p>2$ and $m \geq 3$ is odd, $u_{n,q}^{-}=(q-1)\binom {m}{2}_{q}+q ^{m-1}$ .

Another proof of this result can also be found in [11].

Theorem 1.2 [4, Theorem 1.1].

Let q be the power of a prime number $p>2$ and $n\in \mathbb {N}$ , $n>4$ .

1. (i) If n is odd, then $u_{n,q}^{+}=u_{n,q}^{-}=[\tfrac{n-1}{2}]_{q^2}$ .

2. (ii) If n is even, then there exists $m \in {\mathbb {N^{*}}}$ such that $n=2m$ .

   1. (a) If m is even, $u_{n,q}^{+}=(q-1)\binom {m}{2}_{q}+q^{m-1}$ .

   2. (b) If $m \geq 3$ is odd, $u_{n,q}^{+}=(q-1)\binom {m}{2}_{q}$ .

We will consider the case of the rings ${\mathbb {Z}}/N{\mathbb {Z}}$ , that is to say, we will be interested in the equation $(E_{{\mathbb {Z}}/N{\mathbb {Z}}}):=(E_{N})$ . Note that the resolution of $(E_{N})$ is linked to the different expressions of the elements of the congruence subgroup

$$ \begin{align*}\hat{\Gamma}(N):=\{C \in \text{SL}_{2}(\mathbb{Z}),~C= \pm {\mathrm{Id}}~[N]\}.\end{align*} $$

Indeed, we know that all the matrices of ${\mathrm {SL}}_{2}({\mathbb {Z}})$ can be written in the form $M_{n}(a_1,\ldots ,a_n)$ , with $a_{i}$ a positive integer. Since this expression is not unique, we are naturally led to look for all the expressions of this form for a given matrix or a set of matrices. Note that we already have many results concerning the solutions of $(E_{N})$ (see for example [5, 7]).

Our objective is to obtain the number of $\lambda $ -quiddities of odd size, and an upper and lower bound of the number of $\lambda $ -quiddities of even size, over the rings ${\mathbb {Z}}/2^ {m}{\mathbb {Z}}$ . We will also give a complete formula for ${\mathbb {Z}}/8{\mathbb {Z}}$ . For this, for $n \geq 2$ , $m \geq 2$ and $\epsilon \in \{-1,1\}$ , we write $\Omega _{n}^{\epsilon }(m):=\{(a_{1},\ldots ,a_{n}) \in (\mathbb {Z}/2^{m}\mathbb {Z})^{n},~M_{n}(a_{ 1},\ldots ,a_{n})=\epsilon {\mathrm {Id}}\}$ , $w_{n,2^{m}}^{+}:=|\Omega _{n}^{1}(m) |$ , $w_{n,2^{m}}^{-}:=|\Omega _{n}^{-1}(m)|$ and $w_{n,2^{m}}:=w_{n,2^{m}}^{+}+w_{n,2^{m}}^{-}$ . We already have the following result.

Theorem 1.3 [4, Theorem 1.3].

Let $n\geq 3$ .

1. (i) If n is odd, $w_{n, 4}^{+}=w_{n, 4}^{-}=\tfrac 13(4^{n-2}-2^{n-3})$ .

2. (ii) If n is even, then there exists $m \in {\mathbb {N^{*}}}$ such that $n=2m$ .

   1. (a) If m is even, $w_{n,4}^{+}=\tfrac 13(4^{n-2}+4 \times 2^{n-3})$ and $w_{n,4 }^{-}=\tfrac 13(4^{n-2}- 2^{n-2})$ .

   2. (b) If m is odd, $w_{n,4}^{+}=\tfrac 13(4^{n-2}- 2^{n-2})$ and $w_{n,4}^{ -}=\tfrac 13(4^{n-2}+4 \times 2^{n-3})$ .

We will prove the following two results.

Theorem 1.4. Let $m \geq 2$ and $\epsilon \in \{-1,1\}$ .

1. (i) Let $n \geq 2$ . We have the equality:

   $$ \begin{align*}w_{2n+1,2^{m}}^{+}=w_{2n+1,2^{m}}^{-}=\frac{2^{2mn-2n-2m-1}(2^{2n+3}-8)}{3}.\end{align*} $$

2. (ii) Let $n \geq 3$ . We have the two inequalities:

   1. (a) $|\Omega _{2n}^{\epsilon }(m)| \geq |\Delta _{2n}^{\epsilon }(m)|+2^{m-1}|\Delta _{2n-1}^{\epsilon }(m)|+m2^{m-1}|\Delta _{2n-4}^{\epsilon }(m)|$ ;

   2. (b) $|\Omega _{2n}^{\epsilon }(m)| \leq |\Delta _{2n}^{\epsilon }(m)|+2^{m-1}|\Delta _{2n-1}^{\epsilon }(m)|+2^{2m-2}|\Delta _{2n-1}^{\epsilon }(m)|$ ,

   with $|\Delta _{n}^{\epsilon }(m)|:= 2^{mn-n-3m}(2^{n+1}+8 \times (-1)^{n+1})/3$ .

Theorem 1.5. Let $n \geq 2$ . We have the two formulae:

$$ \begin{align*} w_{2n+1,8}^{+}&=w_{2n+1,8}^{-}=\frac{2^{6n-2n-7}(2^{2n+3}-8)}{3}; \\ w_{2n,8}&=28 \times 8^{n-2}+\frac{2^{4n-5}-2^{3n-3}+2^{6n-6}-2^{3n}}{3}. \end{align*} $$

Theorem 1.4 is proved in Section 2.2 while the proof of Theorem 1.5 is given in Section 2.3. To prove the theorems, we will first focus on the cardinality of the set $\{(a_{1},\ldots ,a_{n}) \in (\mathbb {Z}/2^{m}\mathbb {Z})^{n},~M_{n}(a_{1},\ldots ,a_{n})=\epsilon {\mathrm {Id}}~\mathrm {and}~a_{2}~\mathrm {invertible}\}$ and then relate it to $|\Omega _{n}^{\epsilon }(m)|$ . More precisely, we will construct bijections which will allow us to find some direct or recursive relations satisfied by the desired cardinalities.

2. Proofs of the counting formulae

2.1. Preliminary results

The aim of this section is to provide some elements which will be useful in the proofs of our main theorems. Throughout this section, $U(m):=\{x \in {\mathbb {Z}}/2^{m}{\mathbb {Z}},~x~\mathrm {invertible}\}$ , $\Omega _{n}^{B}(m):=\{(a_{1},\ldots ,a_{n}) \in (\mathbb {Z}/2^{m}\mathbb {Z})^{n},~M_{n}(a_{1},\ldots ,a_{n})=B\}$ .

Proposition 2.1 [4, Lemma 2.16 and Proposition 2.18].

1. (i) Let A be a commutative and unitary ring. Let $n=2l \geq 4$ and $\lambda $ be an invertible element of A. Let $(a_{1},\ldots ,a_{n}) \in A^{n}$ . If $M_{n}(a_{1},\ldots ,a_{n})=\epsilon {\mathrm {Id}}$ , with $\epsilon \in \{1,-1\}$ , then $M_{n}(\lambda a_{1},\lambda ^{-1} a_{2},\ldots ,\lambda a_{2l-1},\lambda ^{-1} a_{2l})=\epsilon {\mathrm {Id}}$ .

2. (ii) Let A be a commutative and unitary ring. Let $n \in {\mathbb {N}}^{*}$ , n odd. The map

   $$ \begin{align*} \varphi_n{:}\ \{(a_{1},\ldots,a_{n}) \in A^{n}, &\ M_{n}(a_{1},\ldots,a_{n})={\mathrm{Id}}\} \\ & \longrightarrow \{(a_{1},\ldots,a_{n}) \in A^{n},~M_{n}(a_{1},\ldots,a_{n})=-{\mathrm{Id}}\} \end{align*} $$
   defined by $(a_{1},\ldots ,a_{n}) \longmapsto (-a_{1},\ldots ,-a_{n})$ is a bijection.

Lemma 2.2. Let A be a commutative and unitary ring, and $(a,b,c,u,v) \in A^{5}$ .

1. (i) $M_{3}(a,1,b)=M_{2}(a-1,b-1)$ .

2. (ii) $M_{3}(a,-1,b)=-M_{2}(a+1,b+1)$ .

3. (iii) Suppose $uv-1$ is invertible. Then

   $$ \begin{align*} M_{4}(a,u,v,b)=M_{3}(a+(1-v)(uv-1)^{-1},uv-1,b+(1-u)(uv-1)^{-1}). \end{align*} $$

4. (iv) Suppose v is invertible and $x=((vb-1)(uv-1)-1)v^{-1}$ is invertible. Then

   $$ \begin{align*} M_{5}(a,u,v,b,c)=M_{3}(a-(vb-2)x^{-1},x,c-(uv-2)x^{-1}). \end{align*} $$

Proof. These formulae can be verified by direct computations. Note that items (i), (ii) and (iii) are given in [3, Section 4]; item (iv) was an important formula obtained by Cuntz during the preparation of [4] (private communication to the author in 2023).

Proposition 2.3. Let $N=2^{m}$ , $m \geq 2$ , $B \in {\mathrm {SL}}_{2}(\mathbb {Z}/N\mathbb {Z})$ and $n>4$ . We define the set $\Delta _{n}^{B}(m):=\{(a_{1},\ldots ,a_{n}) \in (\mathbb {Z}/2^{m}\mathbb {Z})^{n},~M_{n}(a_{1},\ldots ,a_{n})=B~and~a_{2} \in U(m)\}$ . Then

$$ \begin{align*} |\Delta_{n}^{B}(m)|=2^{m-1}|\Delta_{n-1}^{B}(m)|+2^{2m-1}|\Delta_{n-2}^{B}(m)|. \end{align*} $$

Proof. Let $m \geq 2$ , $B \in \text {SL}_{2}(\mathbb {Z}/2^{m}\mathbb {Z})$ and $n>4$ . We begin by defining

• • $\Omega _{n}^{B}(m):=\{(a_{1},\ldots ,a_{n}) \in (\mathbb {Z}/2^{m}\mathbb {Z})^{n},~M_{n}(a_{1},\ldots ,a_{n})=B\}$ ;

• • $\Delta _{n}^{B}(m):=\{(a_{1},\ldots ,a_{n}) \in \Omega _{n}^{B}(m),~a_{2} \in U(m)\}$ ;

• • $\Lambda _{n}^{B}(m,x):=\{(a_{1},\ldots ,a_{n}) \in \Omega _{n}^{B}(m),~a_{2}=x\}$ ;

• • $\psi : U(m) \times U(m) \times \mathbb {Z}/2^{m}\mathbb {Z} \longrightarrow U(m)$ where $ (u,v,w) \longmapsto ((vw-1)(uv-1)-1)v^{-1}$ ;

• • $T(m,x):=\{(u,v,w) \in U(m) \times U(m) \times \mathbb {Z}/2^{m}\mathbb {Z}, \psi (u,v,w)=x\}$ , $x \in U(m)$ .

We have the following equalities:

$$ \begin{align*} \Delta_{n}^{B}(m) &= \bigsqcup_{u \in U(m)} \{(a_{1},\ldots,a_{n}) \in \Omega_{n}^{B}(m),~a_{2}=u\} \\ &= \bigsqcup_{u \in U(m)} \underbrace{\{(a_{1},\ldots,a_{n}) \in \Omega_{n}^{B}(m),~a_{2}=u~\mathrm{and}~a_{3} \notin U(m)\}}_{X_{n}^{B}(u)} \\ & \quad \bigsqcup_{u \in U(m)} \bigsqcup_{v \in U(m)} \underbrace{\{(a_{1},\ldots,a_{n}) \in \Omega_{n}^{B}(m),~a_{2}=u~\mathrm{and}~a_{3}=v\}}_{Y_{n}^{B}(u,v)}. \end{align*} $$

Let $u=a+2^{m}{\mathbb {Z}} \in U(m)$ ( $a\in {\mathbb {Z}}$ ). We consider the sets $X_{n}^{B}(u)$ and $Y_{n}^{B}(u,v)$ separately.

We begin with $X_{n}^{B}(u)$ . Let $v=b+2^{m}\mathbb {Z}$ ( $b \in {\mathbb {Z}}$ ) be a noninvertible element of $\mathbb {Z}/2^{m}\mathbb {Z}$ . Then b is an even integer, so that $ab$ is even and $ab-1$ is odd. Thus, $uv-1 \in U(m)$ . By Lemma 2.2(iii), we can define the following two maps:

• • $f_{n,u} : X_{n}^{B}(u) \longrightarrow \Delta _{n-1}^{B}(m)$ which takes $(a_{1},u,a_{3},\ldots ,a_{n})$ to

  $$ \begin{align*} (a_{1}+(1-a_{3})(ua_{3}-1)^{-1},ua_{3}-1,a_{4}+(1-u)(ua_{3}-1)^{-1},a_{5},\ldots,a_{n}); \end{align*} $$

• • $g_{n,u} : \Delta _{n-1}^{B}(m) \longrightarrow X_{n}^{B}(u)$ which takes $(a_{1},\ldots ,a_{n-1})$ to

  $$ \begin{align*} (a_{1}+(u^{-1}(a_{2}+1)-1)a_{2}^{-1},u,u^{-1}(a_{2}+1),a_{3}+(u-1)a_{2}^{-1},a_{4},\ldots,a_{n-1}). \end{align*} $$

Then $f_{n,u}$ and $g_{n,u}$ are reciprocal bijections, and $|X_{n}^{B}(u)|=|\Delta _{n-1}^{B}(m)|$ .

Next, we consider $Y_{n}^{B}(u,v)$ . Let $v=b+2^{m}{\mathbb {Z}}$ ( $b \in {\mathbb {Z}}$ ) be an invertible element of $\mathbb {Z}/2^{m}\mathbb {Z}$ . We have

$$ \begin{align*} Y_{n}^{B}(u,v)=\bigsqcup_{w \in \mathbb{Z}/2^{m}\mathbb{Z}} \underbrace{\{(a_{1},\ldots,a_{n}) \in \Omega_{n}^{B}(m), a_{2}=u,~a_{3}=v~\mathrm{ and}~a_{4}=w\}}_{Z_{n}^{B}(u,v,w)}. \end{align*} $$

Hence, we will consider the sets $Z_{n}^{B}(u,v,w)$ . Let w be an element of $\mathbb {Z}/2^{m}\mathbb {Z}$ , and a and b odd integers. Then $ab$ is odd and $ab-1$ is even. Hence, $uv-1$ is not invertible. Let ${x=\psi (u,v,w)=((vw-1)(uv-1)-1)v^{-1}}$ . Since $uv-1$ is not invertible, x is invertible. By Lemma 2.2(iv), we can define the following two maps:

• • $h_{n,u,v,w} : Z_{n}^{B}(u,v,w) \longrightarrow \Lambda _{n-2}^{B}(m,x)$ where

  $$ \begin{align*} (a_{1},u,v,w,a_{5},\ldots,a_{n}) \longmapsto (a_{1}-(vw-2)x^{-1},x,a_{5}-(uv-2)x^{-1},a_{6},\ldots,a_{n});\end{align*} $$

• • $k_{n,u,v,w} : \Lambda _{n-2}^{B}(m,x) \longrightarrow Z_{n}^{B}(u,v,w)$ where

  $$ \begin{align*} (a_{1},\ldots,a_{n-2}) \longmapsto (a_{1}+(vw-2)x^{-1},u,v,w,a_{3}+(uv-2)x^{-1},a_{4},\ldots,a_{n-2}).\end{align*} $$

Then $h_{n,u,v,w}$ and $k_{n,u,v,w}$ are reciprocal bijections. Hence, $|Z_{n}^{B}(u,v,w)|=|\Lambda _{n-2}^{B}(m,x)|$ .

Now, we give some properties of the sets $T(m,x)$ . First,

$$ \begin{align*}U(m) \times U(m) \times (\mathbb{Z}/2^{m}\mathbb{Z})=\bigsqcup_{x \in U(m)} \{(u,v,w) \in U(m) \times U(m) \times \mathbb{Z}/2^{m}\mathbb{Z}, \psi(u,v,w)=x\}.\end{align*} $$

Let $x \in U(m)$ . We define two maps:

$$ \begin{align*}\begin{array}{ccccc} \alpha_{x} : & T(m,1) & \longrightarrow & T(m,x) \\ & (u,v,w) & \longmapsto & (ux,vx^{-1},wx) \\ \end{array} \quad \begin{array}{ccccc} \beta_{x} : & T(m,x) & \longrightarrow & T(m,1) \\ & (u,v,w) & \longmapsto & (ux^{-1},vx,wx^{-1}) \\ \end{array}\!\!{.}\end{align*} $$

Then $\alpha _{x}$ and $\beta _{x}$ are reciprocal bijections, so $|T(m,x)|=|T(m,1)|$ . Moreover,

$$ \begin{align*}2^{3m-2}=|U(m) \times U(m) \times (\mathbb{Z}/2^{m}\mathbb{Z})|=\sum_{x \in U(m)} |T(m,x)|=2^{m-1}|T(m,1)|.\end{align*} $$

So, $|T(m,x)|=|T(m,1)|=2^{2m-1}$ .

If we collect all these observations,

$$ \begin{align*} |\Delta_{n}^{B}(m)| &= \sum_{u \in U(m)} |X_{n}^{B}(u)|+\sum_{u, v \in U(m)} |Y_{n}^{B}(u,v)| \\ &= \sum_{u \in U(m)} |\Delta_{n-1}^{B}(m)|+\sum_{u, v \in U(m)} \bigg(\sum_{w \in \mathbb{Z}/2^{m}\mathbb{Z}} |Z_{n}^{B}(u,v,w)|\bigg) \\ &= |U(m)||\Delta_{n-1}^{B}(m)|+\sum_{x \in U(m)} \bigg(\sum_{(u,v,w) \in T(m,x)} |Z_{n}^{B}(u,v,w)|\bigg) \\ &= 2^{m-1} |\Delta_{n-1}^{B}(m)|+\sum_{x \in U(m)} \bigg(\sum_{(u,v,w) \in T(m,x)} |\Lambda_{n-2}^{B}(m,x)|\bigg) \\ &= 2^{m-1} |\Delta_{n-1}^{B}(m)|+\sum_{x \in U(m)} |T(m,x)| |\Lambda_{n-2}^{B}(m,x)| \\ &= 2^{m-1}|\Delta_{n-1}^{B}(m)|+|T(m,1)|\sum_{x \in U(m)} |\Lambda_{n-2}^{B}(m,x)| \\ &= 2^{m-1} |\Delta_{n-1}^{B}(m)|+|T(m,1)||\Delta_{n-2}^{B}(m)| \\ &= 2^{m-1} |\Delta_{n-1}^{B}(m)|+2^{2m-1}|\Delta_{n-2}^{B}(m)|.\\[-3pc] \end{align*} $$

Remark 2.4. Let $x \neq y$ be two invertible elements of $\mathbb {Z}/2^{m}\mathbb {Z}$ . In general, $|\Lambda _{n}^{B}(m,x)| \neq |\Lambda _{n}^{B}(m,y)|$ . For instance, by computation, we find the following values: ${|\Lambda _{5}^{{\mathrm {Id}}}(3,1+8\mathbb {Z})|=20}$ and $|\Lambda _{5}^{{\mathrm {Id}}}(3,3+8\mathbb {Z})|=8$ .

Proposition 2.5. Let $N=2^{m}$ , $m \geq 2$ , $B \in {\mathrm {SL}}_{2}(\mathbb {Z}/N\mathbb {Z})$ and $n>4$ . We define the set $\Delta _{n}^{B}(m):=\{(a_{1},\ldots ,a_{n}) \in (\mathbb {Z}/N\mathbb {Z})^{n},~M_{n}(a_{1},\ldots ,a_{n})=B~and~a_{2} \in U(m)\}$ . Then

$$ \begin{align*}|\Delta_{n}^{B}(m)|=\frac{2^{mn-n-4m+1}(2^{n}+(-1)^{n}\times 8)}{3}|\Delta_{4}^{B}(m)|+\frac{2^{mn-n-3m}(2^{n}+(-1)^{n+1}\times 16)}{3}|\Delta_{3}^{B}(m)|.\end{align*} $$

Proof. We set

$$ \begin{align*}A=\begin{pmatrix} 2^{m-1} & 2^{2m-1} \\ 1 & 0 \end{pmatrix} \quad\mbox{and}\quad P=\begin{pmatrix} 1 & 1 \\ \dfrac{1}{2^{m}} & \dfrac{-1}{2^{m-1}} \end{pmatrix}, \quad\mbox{so that } P^{-1}=\frac{-2^{m}}{3}\begin{pmatrix} \dfrac{-1}{2^{m-1}} & -1 \\ \dfrac{-1}{2^{m}} & 1 \end{pmatrix}. \end{align*} $$

By the previous proposition,

$$ \begin{align*}\begin{pmatrix} |\Delta_{n}^{B}(m)| \\[2.5pt] |\Delta_{n-1}^{B}(m)| \end{pmatrix}=\begin{pmatrix} 2^{m-1} & 2^{2m-1} \\[2.5pt] 1 & 0 \end{pmatrix}\begin{pmatrix} |\Delta_{n-1}^{B}(m)| \\[2.5pt] |\Delta_{n-2}^{B}(m)| \end{pmatrix}=A^{n-4}\begin{pmatrix} |\Delta_{4}^{B}(m)| \\[2.5pt] |\Delta_{3}^{B}(m)| \end{pmatrix}.\end{align*} $$

Moreover, $A=P\big (\begin {smallmatrix} 2^{m} & 0 \\ 0 & -2^{m-1} \end {smallmatrix}\big )P^{-1}$ . Hence,

$$ \begin{align*} |\Delta_{n}^{B}(m)|&=\frac{2^{mn-n-4m+1}(2^{n}+(-1)^{n}\times 8)}{3}|\Delta_{4}^{B}(m)|\\ &\quad+\frac{2^{mn-n-3m}(2^{n}+(-1)^{n+1}\times 16)}{3}|\Delta_{3}^{B}(m)|.\\[-3.2pc] \end{align*} $$

Let $S:=(\begin {smallmatrix} 0 & -1 \\ 1 & 0 \end {smallmatrix}$ ) and $T:=(\begin {smallmatrix} 1 & 1 \\ 0 & 1 \end {smallmatrix}$ ). Then ${\mathrm {SL}}_{2}(\mathbb {Z})$ is generated by S and T and we have $M_{n}(a_{1},\ldots ,a_{n})=T^{a_{n}}S\cdots T^{a_{1}}S$ for all $(a_{1},\ldots ,a_{n}) \in {\mathbb {Z}}^{n}$ .

Corollary 2.6. Let $m \geq 2$ and $n>4$ . Then

$$ \begin{align*} |\Delta_{n}^{{\mathrm{Id}}}(m)|=|\Delta_{n}^{-{\mathrm{Id}}}(m)| & =\frac{2^{mn-n-3m}(2^{n+1}+8 \times (-1)^{n+1})}{3}; \\ |\Delta_{n}^{S}(m)|=|\Delta_{n}^{-S}(m)| & =\frac{2^{mn-n-3m+1}(2^{n}+(-1)^{n}\times 8)}{3}; \\ |\Delta_{n}^{T}(m)|=|\Delta_{n}^{-T}(m)|=|\Delta_{n}^{{\mathrm{Id}}}(m)| & =\frac{2^{mn-n-3m}(2^{n+1}+8 \times (-1)^{n+1})}{3}. \end{align*} $$

Proof. We apply the formula given in the previous proposition with the following values:

$$ \begin{align*} |\Delta_{4}^{{\mathrm{Id}}}(m)|=|\Delta_{4}^{-{\mathrm{Id}}}(m)|=2^{m-1}, &\quad |\Delta_{3}^{{\mathrm{Id}}}(m)|=|\Delta_{3}^{-{\mathrm{Id}}}(m)|=1; \\ |\Delta_{4}^{S}(m)|=|\Delta_{4}^{-S}(m)|=2^{m}, &\quad |\Delta_{3}^{S}(m)|=|\Delta_{3}^{-S}(m)|=0; \\ |\Delta_{4}^{T}(m)|=|\Delta_{4}^{-T}(m)|=2^{m-1}, &\quad |\Delta_{3}^{T}(m)|=|\Delta_{3}^{-T}(m)|=1.\\[-2.6pc] \end{align*} $$

For instance, we have the values shown in Table 1.

Table 1 Numerical values of $|\Delta_n^{\mathrm{Id}}(3)|$ and $|\Delta_n^S(3)|$ for small values of $n$ .

Proposition 2.7. Let $N=2^{m}$ , $m \geq 2$ , $B \in {\mathrm {SL}}_{2}(\mathbb {Z}/N\mathbb {Z})$ and $n \geq 3$ . We define the set $\Lambda _{n}^{B}(m,-1):=\{(a_{1},\ldots ,a_{n}) \in \Omega _{n}^{B}(m),~a_{2}=-1\}$ . Then $|\Lambda _{n}^{B}(m,-1)|=|\Omega _{n-1}^{-B}(m)|$ .

Proof. By Lemma 2.2(ii), $(a_{1},\ldots ,a_{n}) \in \Lambda _{n}^{B}(m,-1) \mapsto (a_{1}+1,a_{3}+1,a_{4},\ldots ,a_{n}) \in \Omega _{n-1}^{-B}(m)$ is a bijection.

Lemma 2.8. Let $m \geq 2$ . Then $|\{(x,y) \in ((\mathbb {Z}/2^{m}\mathbb {Z})-U(m))^{2},~xy=0\}|=m2^{m-1}$ .

Proof. We have the following equalities:

$$ \begin{align*} R &= \{(x,y) \in ((\mathbb{Z}/2^{m}\mathbb{Z})-U(m))^{2},~xy=0\} \\ &= \{(0,y),~y \in (\mathbb{Z}/2^{m}\mathbb{Z})-U(m)\} \sqcup \{(x,0),~x \in (\mathbb{Z}/2^{m}\mathbb{Z})-U(m)~\mathrm{and}~x \neq 0\} \\ & \quad \sqcup \{(2^{k}a+2^{m}\mathbb{Z},2^{l}b+2^{m}\mathbb{Z}),~1 \leq k \leq m-1,~m-k \leq l \leq m-1, \\ & \qquad\qquad a,b~\mathrm{odd}, 0< 2^{k}a, 2^{l}b <2^{m} \}. \end{align*} $$

Hence,

$$ \begin{align*} |R| &= 2^{m-1}+2^{m-1}-1+\sum_{k=1}^{m-1} 2^{m-k-1} \sum_{l=m-k}^{m-1} 2^{m-l-1} \\ &= 2^{m}-1+2^{2m-2}\sum_{k=1}^{m-1} \frac{1}{2^{k}} \frac{2}{2^{m-k}}(1-2^{-k}) \\ &= 2^{m}-1+2^{m-1}(m-1-(1-2^{-m+1})) = m2^{m-1}.\\[-2.8pc] \end{align*} $$

Proposition 2.9. Let $m \geq 2$ . Then $w_{4,2^{m}}^{+}=(m+2)2^{m-1}$ , $w_{4,2^{m}}^{-}=2^{m}$ .

Proof. (i) $\Omega _{4}^{1}(m)=\{(-y,x,y,-x) \in (\mathbb {Z}/2^{m}\mathbb {Z})^{4},~xy=0\}$ . Hence, by the previous lemma,

$$ \begin{align*} |\Omega_{4}^{1}(m)| = |\{(x,y) \in ((\mathbb{Z}/2^{m}\mathbb{Z}) -U(m))^{2}, xy=0\}| & +|\{(x,0), x \in U(m)\}| \\ &+|\{(0,y), y \in U(m)\}| = (m+2)2^{m-1}. \end{align*} $$

(ii) $\Omega _{4}^{-1}(m)=\{(y,x,y,x) \in (\mathbb {Z}/2^{m}\mathbb {Z})^{4},~xy=2+2^{m}\mathbb {Z}\}$ . Let $x=2a+2^{m}\mathbb {Z}$ and $y=2b+2^{m}\mathbb {Z}$ , $(a,b) \in \mathbb {Z}^{2}$ . Then $xy=4ab+2^{m}\mathbb {Z} \neq 2+2^{m}\mathbb {Z}$ since $4ab-2$ is not a multiple of $2^{m}$ ( $m \geq 2$ ). So, $xy=2$ implies $x \in U(m)$ or $y \in U(m)$ . Hence,

$$ \begin{align*} |\Omega_{4}^{-1}(m)\| = |\{(-2x^{-1},x,2x^{-1},-x),x \in U(m)\}|&+|\{(-y,2y^{-1},y,-2y^{-1}), y \in U(m)\}|=2^{m}.\\[-2pc] \end{align*} $$

2.2. Proof of Theorem 1.4

Let $N=2^{m}$ , $m \geq 2$ , $n \geq 2$ and $\epsilon =\pm 1$ . Define the sets:

• • $\Omega _{n}^{\epsilon }(m):=\{(a_{1},\ldots ,a_{n}) \in (\mathbb {Z}/2^{m}\mathbb {Z})^{n},~M_{n}(a_{1},\ldots ,a_{n})=\epsilon {\mathrm {Id}}\}$ ;

• • $\Delta _{n}^{\epsilon }(m):=\{(a_{1},\ldots ,a_{n}) \in (\mathbb {Z}/2^{m}\mathbb {Z})^{n},~M_{n}(a_{1},\ldots ,a_{n})=\epsilon {\mathrm {Id}}~\mathrm {and}~a_{2} \in U(m)\}$ ;

• • $\Lambda _{n}^{\epsilon }(m,u)=\{(a_{1},\ldots ,a_{n}) \in \Omega _{n}^{\epsilon }(m),~a_{2}=u\}$ for $u \in U(m)$ .

(i) By Proposition 2.1(i) and Lemma 2.2(i), we can define the maps:

$$ \begin{align*} \begin{array}{ccccc} \vartheta_{n,u} : & \Lambda_{2n}^{\epsilon}(m,u) & \longrightarrow & \Omega_{2n-1}^{\epsilon}(m) \\ & (a_{1},u,a_{3},\ldots,a_{2n}) & \longmapsto & (a_{1}u-1,a_{3}u-1,a_{4}u^{-1},a_{5}u,\ldots,a_{2n}u^{-1}) \\ \end{array} \end{align*} $$

$$ \begin{align*} \begin{array}{ccccc} \theta_{n,u} : & \Omega_{2n-1}^{\epsilon}(m) & \longrightarrow & \Lambda_{2n}^{\epsilon}(m,u) \\ & (a_{1},\ldots,a_{2n-1}) & \longmapsto & ((a_{1}+1)u^{-1},u,(a_{2}+1) u^{-1},a_{3}u,\ldots,a_{2n-1}u) \\ \end{array}\!{.} \end{align*} $$

Then $\vartheta _{n,u}$ and $\theta _{n,u}$ are reciprocal bijections. Hence, $|\Omega _{2n-1}^{\epsilon }(m)|=|\Lambda _{2n}^{\epsilon }(m,u)|$ and so $|\Lambda _{2n}^{\epsilon }(m,u)|= |\Lambda _{2n}^{\epsilon }(m,v)|$ for all $u,v \in U(m)$ .

Moreover, $|\Delta _{2n}^{\epsilon }(m)|=\sum _{u \in U(m)} |\Lambda _{2n}^{\epsilon }(m,u)|=2^{m-1}|\Omega _{2n-1}^{\epsilon }(m)|$ . By Corollary 2.6,

$$ \begin{align*} w_{2n-1,2^{m}}^{+}=|\Omega_{2n-1}^{1}(m)|=\frac{2^{2mn-2n-3m}(2^{2n+1}+8 \times(-1)^{2n+1})}{3\times 2^{m-1}}=\frac{2^{2mn-2n-4m+1}(2^{2n+1}-8)}{3}. \end{align*} $$

So, by Proposition 2.1(ii),

$$ \begin{align*} w_{2n+1,2^{m}}^{+}=w_{2n+1,2^{m}}^{-}=\frac{2^{2mn-2n-2m-1}(2^{2n+3}-8)}{3}. \end{align*} $$

(ii) Let $n \geq 3$ . We have the equality:

$$ \begin{align*} \Omega_{2n}^{\epsilon}(m) &= \Delta_{2n}^{\epsilon}(m) \bigsqcup_{x \notin U(m)}\bigsqcup_{y \in \mathbb{Z}/2^{m}\mathbb{Z}} \underbrace{\{(a_{1},\ldots,a_{2n}) \in \Omega_{2n}^{\epsilon}(m),~a_{2}=x,~a_{3}=y\}}_{G_{2n}^{\epsilon}(x,y)} \\&= \Delta_{2n}^{\epsilon}(m) \bigsqcup_{x \notin U(m)}\bigsqcup_{y \in U(m)} G_{2n}^{\epsilon}(x,y) \bigsqcup_{x \notin U(m)}\bigsqcup_{y \notin U(m)} G_{2n}^{\epsilon}(x,y). \end{align*} $$

Let $x=a+2^{m}\mathbb {Z}$ ( $a \in \mathbb {Z}$ ) be a noninvertible element of $\mathbb {Z}/2^{m}\mathbb {Z}$ . Let $y=b+2^{m}\mathbb {Z}$ ( $b \in \mathbb {Z}$ ). Then a is an even integer, so $ab$ is even and $ab-1$ is odd. Thus, $xy-1 \in U(m)$ . By Lemma 2.2(iii), we can define the two maps: $\sigma _{n,x,y} : G_{2n}^{\epsilon }(x,y) \longrightarrow \Lambda _{2n-1}^{\epsilon }(m,xy-1)$ where

$$ \begin{align*} (a_{1},x,y,a_{4},\ldots,a_{2n})\longmapsto (a_{1}\!+\!(1\!-\!y)(xy\!-\!1)^{-1},xy-1,a_{4}\!+\!(1\!-\!x)(xy-1)^{-1}, a_{5},\ldots,a_{2n}) \end{align*} $$

and $\tau _{n,x,y} : \Lambda _{2n-1}^{\epsilon }(m,xy-1) \longrightarrow G_{2n}^{\epsilon }(x,y)$ where

$$ \begin{align*} (a_{1},xy-1, &\ a_{3},\ldots,a_{2n-1}) \\ & \longmapsto (a_{1}-(1-y)(xy-1)^{-1},x,y,a_{3}-(1-x)(xy-1)^{-1}, a_{4},\ldots,a_{2n-1}). \end{align*} $$

Then $\sigma _{n,x,y}$ and $\tau _{n,x,y}$ are reciprocal bijections. Hence, $|G_{2n}^{\epsilon }(x,y)|=|\Lambda _{2n-1}^{\epsilon }(m,xy-1)|$ .

Let $y \in U(m)$ . Then $x \in (\mathbb {Z}/2^{m}\mathbb {Z}-U(m)) \mapsto xy-1 \in U(m)$ is a bijection. Indeed, let $z \in U(m)$ . The equation $xy-1=z$ has exactly one solution, $x=(z+1)y^{-1}$ , in $(\mathbb {Z}/2^{m}\mathbb {Z})-U(m)$ . Hence,

$$ \begin{align*} \bigg|\bigsqcup_{x \notin U(m)}\bigsqcup_{y \in U(m)} G_{2n}^{\epsilon}(x,y)\bigg| &= \sum_{y \in U(m)} \sum_{x \notin U(m)} |G_{2n}^{\epsilon}(x,y)| = \sum_{y \in U(m)} \sum_{x \notin U(m)} |\Lambda_{2n-1}^{\epsilon}(m,xy-1)| \\ &= \sum_{y \in U(m)} \sum_{z \in U(m)} |\Lambda_{2n-1}^{\epsilon}(m,z)| = \sum_{y \in U(m)} |\Delta_{2n-1}^{\epsilon}(m)|\\ &= 2^{m-1}|\Delta_{2n-1}^{\epsilon}(m)|. \end{align*} $$

Moreover,

$$ \begin{align*}\bigg|\bigsqcup_{x,y \notin U(m)} G_{2n}^{\epsilon}(x,y)\bigg|=\sum_{x,y \notin U(m)} |G_{2n}^{\epsilon}(x,y)|=\sum_{x,y \notin U(m)} |\Lambda_{2n-1}^{\epsilon}(m,xy-1)|. \end{align*} $$

So,

$$ \begin{align*}\bigg|\bigsqcup_{x,y \notin U(m)} G_{2n}^{\epsilon}(x,y)\bigg| \leq \sum_{x,y \notin U(m)} |\Delta_{2n-1}^{\epsilon}(m)|=2^{2m-2}|\Delta_{2n-1}^{\epsilon}(m)|.\end{align*} $$

In addition,

$$ \begin{align*}\bigg|\bigsqcup_{x,y \notin U(m)} G_{2n}^{\epsilon}(x,y)\bigg| \geq \bigg|\bigsqcup_{x,y \notin U(m), xy=0} G_{2n}^{\epsilon}(x,y)\bigg| \geq m2^{m-1}|\Delta_{2n-4}^{\epsilon}(m)|.\end{align*} $$

Indeed, let $x,y$ be two noninvertible elements of $\mathbb {Z}/2^{m}\mathbb {Z}$ satisfying $xy=0$ . Then $(-y,x,y,-x) \in \Omega _{4}^{1}(m)$ . For all elements $(a_{1},\ldots ,a_{2n-4}) \in \Delta _{2n-4}^{\epsilon }(m)$ , we have $(-y,x,y,-x,a_{1},\ldots , a_{2n-4}) \in G_{2n}^{\epsilon }(x,y)$ . So, $|G_{2n}^{\epsilon }(x,y)| \geq |\Delta _{2n-4}^{\epsilon }(m)|$ . By combining this with the result of Lemma 2.8, we reach the desired inequality.

Hence,

$$ \begin{align*} &|\Delta_{2n}^{\epsilon}(m)|+2^{m-1} |\Delta_{2n-1}^{\epsilon}(m)| +m2^{m-1}|\Delta_{2n-4}^{\epsilon}(m)| \\ &\quad \leq |\Omega_{2n}^{\epsilon}(m)| \leq |\Delta_{2n}^{\epsilon}(m)|+2^{m-1}|\Delta_{2n-1}^{\epsilon}(m)|+2^{2m-2}|\Delta_{2n-1}^{\epsilon}(m)|. \end{align*} $$

If we associate this inequality with the formula given in Corollary 2.6, we have the result given in the theorem.

2.3. The case of $\boldsymbol {\mathbb {Z}/8\mathbb {Z}}$

The aim of this section is to prove Theorem 1.5. We use the notation introduced in the previous section.

We already have the formula for $w_{2n+1,8}^{+}=w_{2n+1,8}^{-}$ . Let $n \geq 3$ and $\epsilon \in \{-1,1\}$ . We will focus on $|\Omega _{2n}^{\epsilon }(3)|+|\Omega _{2n}^{-\epsilon }(3)|$ . The proof of Theorem 1.4 gives us the following formula:

$$ \begin{align*} |\Omega_{2n}^{\epsilon}(3)|=|\Delta_{2n}^{\epsilon}(3)|+4|\Delta_{2n-1}^{\epsilon}(3)|+\sum_{x,y \notin U(3)} |\Lambda_{2n-1}^{\epsilon}(3,xy-1)|. \end{align*} $$

To give a complete formula, we have to study the value of $\sum _{x,y \notin U(3)} |\Lambda _{2n-1}^{\epsilon }(3,xy-1)|$ . To do this, we will use the different possible values of $xy-1$ ( $x,y \notin U(3)$ ) given in Table 2.

Table 2 Different possible values of $xy-1$ for $x,y$ noninvertible elements of $\mathbb{Z}/8\mathbb{Z}$ .

From Table 2,

$$ \begin{align*}\sum_{x,y \notin U(3)} |\Lambda_{2n-1}^{\epsilon}(3,xy-1)|=12| \Lambda_{2n-1}^{\epsilon}(3,-1+8\mathbb{Z})|+4| \Lambda_{2n-1}^{\epsilon}(3,3+8\mathbb{Z})|.\end{align*} $$

Hence,

$$ \begin{align*} w_{2n,8} &= |\Omega_{2n}^{\epsilon}(3)|+|\Omega_{2n}^{-\epsilon}(3)| \\ &= |\Delta_{2n}^{\epsilon}(3)|+4|\Delta_{2n-1}^{\epsilon}(3)|+12| \Lambda_{2n-1}^{\epsilon}(3,-1+8\mathbb{Z})| +4| \Lambda_{2n-1}^{\epsilon}(3,3+8\mathbb{Z})|+ |\Delta_{2n}^{-\epsilon}(3)|\\ &\quad +4|\Delta_{2n-1}^{-\epsilon}(3)|+12| \Lambda_{2n-1}^{-\epsilon}(3,-1+8\mathbb{Z})|+4| \Lambda_{2n-1}^{-\epsilon}(3,3+8\mathbb{Z})|. \end{align*} $$

For $x \in U(m)$ , the map $(a_{1},\ldots ,a_{2n-1}) \in \Lambda _{2n-1}^{-\epsilon }(3,x) \mapsto (-a_{1},\ldots ,-a_{2n-1}) \in \Lambda _{2n-1}^{\epsilon }(3,-x)$ is a bijection (by Proposition 2.1(ii)). Thus, $| \Lambda _{2n-1}^{-\epsilon }(3,x)|=| \Lambda _{2n-1}^{\epsilon }(3,-x)|$ . Besides, by Corollary 2.6, $|\Delta _{l}^{\epsilon }(3)|=|\Delta _{l}^{-\epsilon }(3)|$ for all $l \geq 5$ . Hence,

$$ \begin{align*} w_{2n,8} &= 2|\Delta_{2n}^{\epsilon}(3)|+8|\Delta_{2n-1}^{\epsilon}(3)|+12| \Lambda_{2n-1}^{\epsilon}(3,-1+8\mathbb{Z})|+4| \Lambda_{2n-1}^{\epsilon}(3,3+8\mathbb{Z})| \\ &\quad +12| \Lambda_{2n-1}^{-\epsilon}(3,-1+8\mathbb{Z})|+4| \Lambda_{2n-1}^{\epsilon}(3,5+8\mathbb{Z})| \\ &= 2|\Delta_{2n}^{\epsilon}(3)|+8|\Delta_{2n-1}^{\epsilon}(3)|+12| \Lambda_{2n-1}^{\epsilon}(3,-1+8\mathbb{Z})|+4|\Delta_{2n-1}^{\epsilon}(3)| \\ &\quad +12| \Lambda_{2n-1}^{-\epsilon}(3,-1+8\mathbb{Z})|-4| \Lambda_{2n-1}^{\epsilon}(3,1+8\mathbb{Z})|-4| \Lambda_{2n-1}^{\epsilon}(3,-1+8\mathbb{Z})| \\ &= 2|\Delta_{2n}^{\epsilon}(3)|+12|\Delta_{2n-1}^{\epsilon}(3)|+12| \Lambda_{2n-1}^{\epsilon}(3,-1+8\mathbb{Z})|+12| \Lambda_{2n-1}^{-\epsilon}(3,-1+8\mathbb{Z})| \\ &\quad -4| \Lambda_{2n-1}^{-\epsilon}(3,-1+8\mathbb{Z})|-4| \Lambda_{2n-1}^{\epsilon}(3,-1+8\mathbb{Z})| \\ &= 2|\Delta_{2n}^{\epsilon}(3)|+12|\Delta_{2n-1}^{\epsilon}(3)|+8| \Lambda_{2n-1}^{\epsilon}(3,-1+8\mathbb{Z})|+8| \Lambda_{2n-1}^{-\epsilon}(3,-1+8\mathbb{Z})| \\ &= 2|\Delta_{2n}^{\epsilon}(3)|+12|\Delta_{2n-1}^{\epsilon}(3)|+8w_{2n-2,8} \quad(\mbox{by Proposition}~{2.7}). \end{align*} $$

Hence, by Corollary 2.6,

$$ \begin{align*} w_{2n,8} &= 8^{n-2}w_{4,8}+\sum_{k=0}^{n-3} 8^{k}\frac{2^{4(n-k)-6}+7\times 2^{6(n-k)-9}}{3} \\ &= 28 \times 8^{n-2}+\frac{2^{4n-6}}{3}\sum_{k=0}^{n-3} \bigg(\frac{1}{2}\bigg)^{k} +\frac{7\times 2^{6n-9}}{3}\sum_{k=0}^{n-3} \bigg(\frac{1}{8}\bigg)^{k} \\ &= 28 \times 8^{n-2}+\frac{2^{4n-5}}{3}(1-2^{2-n}) +\frac{2^{6n-6}}{3}(1-2^{6-3n}) \\ &= 28 \times 8^{n-2}+\frac{2^{4n-5}-2^{3n-3}+2^{6n-6}-2^{3n}}{3}. \end{align*} $$

This formula is already true for $n=2$ . This completes the proof of Theorem 1.5.

2.4. Numerical applications

We can also establish other formulae. Indeed, with the Chinese remainder theorem, we can easily prove the following results.

Corollary 2.10. Let $k=p_{1}\ldots p_{r}$ with $p_{i}$ distinct odd prime numbers. For $m \geq 2$ and $n \geq 2$ ,

$$ \begin{align*} w_{n,2^{m}k}^{+} & =|\{(a_{1},\ldots,a_{n})\in ({\mathbb{Z}}/2^{m}k{\mathbb{Z}})^{n},~M_{n}(a_{1},\ldots,a_{n})={\mathrm{Id}}\}|=w_{n,2^{m}}^{+}u_{n,p_{1}}^{+}u_{n,p_{2}}^{+}\ldots u_{n,p_{r}}^{+}, \\ w_{n,2^{m}k}^{-} & =|\{(a_{1},\ldots,a_{n})\in ({\mathbb{Z}}/2^{m}k{\mathbb{Z}})^{n},~M_{n}(a_{1},\ldots,a_{n})=-{\mathrm{Id}}\}|=w_{n,2^{m}}^{-}u_{n,p_{1}}^{-}u_{n,p_{2}}^{-}\ldots u_{n,p_{r}}^{-}. \end{align*} $$

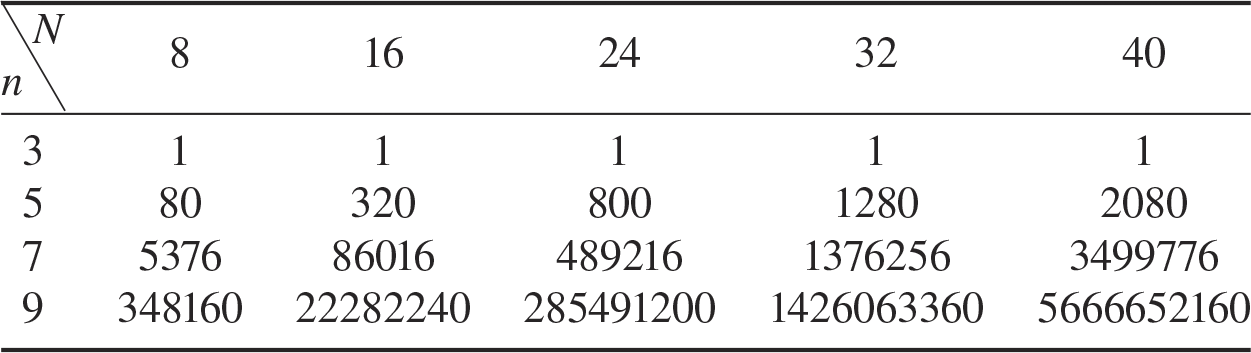
We give some values obtained with the formulae given in Theorems 1.4 and 1.5 in Table 3. We begin with $w_{n,N}^{+}$ for n odd.

Table 3 Numerical values of $w_{n,N}^+$ for some values of $n$ and $N$ .

Finally, we consider $w_{n,8}$ in Table 4.

Table 4 Numerical values of $w_{n,8}$ for small values of $n$ .