Article contents
Some Engel conditions on infinite subsets of certain groups
Published online by Cambridge University Press: 17 April 2009
Abstract
Let k be a positive integer. We denote by ɛk(∞) the class of all groups in which every infinite subset contains two distinct elements x, y such that [x,k y] = 1. We say that a group G is an 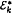 -group provided that whenever X, Y are infinite subsets of G, there exists x ∈ X, y ∈ Y such that [x,k y] = 1. Here we prove that:
-group provided that whenever X, Y are infinite subsets of G, there exists x ∈ X, y ∈ Y such that [x,k y] = 1. Here we prove that:
(1) If G is a finitely generated soluble group, then G ∈ ɛ3(∞) if and only if G is finite by a nilpotent group in which every two generator subgroup is nilpotent of class at most 3.
(2) If G is a finitely generated metabelian group, then G ∈ ɛk(∞) if and only if G/Zk (G) is finite, where Zk (G) is the (k + 1)-th term of the upper central series of G.
(3) If G is a finitely generated soluble ɛk(∞)-group, then there exists a positive integer t depending only on k such that G/Zt (G) is finite.
(4) If G is an infinite 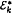 -group in which every non-trivial finitely generated subgroup has a non-trivial finite quotient, then G is k-Engel. In particular, G is locally nilpotent.
-group in which every non-trivial finitely generated subgroup has a non-trivial finite quotient, then G is k-Engel. In particular, G is locally nilpotent.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 2000
References
- 5
- Cited by


