Published online by Cambridge University Press: 04 March 2022
The
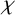 $\chi $
-stability index
$\chi $
-stability index
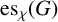 $\mathrm {es}_{\chi }(G)$
of a graph G is the minimum number of its edges whose removal results in a graph with chromatic number smaller than that of G. We consider three open problems from Akbari et al. [‘Nordhaus–Gaddum and other bounds for the chromatic edge-stability number’, European J. Combin. 84 (2020), Article no. 103042]. We show by examples that a known characterisation of k-regular (
$\mathrm {es}_{\chi }(G)$
of a graph G is the minimum number of its edges whose removal results in a graph with chromatic number smaller than that of G. We consider three open problems from Akbari et al. [‘Nordhaus–Gaddum and other bounds for the chromatic edge-stability number’, European J. Combin. 84 (2020), Article no. 103042]. We show by examples that a known characterisation of k-regular (
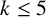 $k\le 5$
) graphs G with
$k\le 5$
) graphs G with
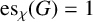 $\mathrm {es}_{\chi }(G) = 1$
does not extend to
$\mathrm {es}_{\chi }(G) = 1$
does not extend to
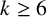 $k\ge 6$
, and we characterise graphs G with
$k\ge 6$
, and we characterise graphs G with
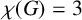 $\chi (G)=3$
for which
$\chi (G)=3$
for which
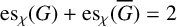 $\mathrm { es}_{\chi }(G)+\mathrm {es}_{\chi }(\overline {G}) = 2$
. We derive necessary conditions on graphs G which attain a known upper bound on
$\mathrm { es}_{\chi }(G)+\mathrm {es}_{\chi }(\overline {G}) = 2$
. We derive necessary conditions on graphs G which attain a known upper bound on
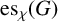 $\mathrm { es}_{\chi }(G)$
in terms of the order and the chromatic number of G and show that the conditions are sufficient when
$\mathrm { es}_{\chi }(G)$
in terms of the order and the chromatic number of G and show that the conditions are sufficient when
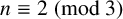 $n\equiv 2 \pmod 3$
and
$n\equiv 2 \pmod 3$
and
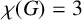 $\chi (G)=3$
.
$\chi (G)=3$
.
Huang was partially supported by the National Natural Science Foundation of China (11801284) and the Fundamental Research Funds for the Central Universities, Nankai University. Lei, Lian and Shi were partially supported by the China–Slovenia bilateral project ‘Some topics in modern graph theory’ (No. 12-6), the National Natural Science Foundation of China and the Fundamental Research Funds for the Central Universities, Nankai University. Klavžar acknowledges the financial support from the Slovenian Research Agency (research core funding No. P1-0297 and projects J1-9109, J1-1693, N1-0095, N1-0108).