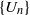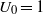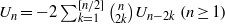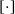Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wang, Haiqing
and
Liu, Guodong
2013.
Some Properties of a Sequence Similar to Generalized Euler Numbers.
ISRN Discrete Mathematics,
Vol. 2013,
Issue. ,
p.
1.
Kang, Jung Yoog
and
Ryoo, Cheon Seoung
2014.
A research on the new polynomials involved with the central factorial numbers, Stirling numbers and others polynomials.
Journal of Inequalities and Applications,
Vol. 2014,
Issue. 1,
Sun, Zhi-Hong
2015.
Super congruences concerning Bernoulli polynomials.
International Journal of Number Theory,
Vol. 11,
Issue. 08,
p.
2393.
Sun, Zhi-Hong
2016.
Supercongruences involving Bernoulli polynomials.
International Journal of Number Theory,
Vol. 12,
Issue. 05,
p.
1259.