 $\ell _{p}$ SPACES
$\ell _{p}$ SPACESPublished online by Cambridge University Press: 03 August 2015
We use the best constants in the Khintchine inequality to generalise a theorem of Kato [‘Similarity for sequences of projections’, Bull. Amer. Math. Soc.73(6) (1967), 904–905] on similarity for sequences of projections in Hilbert spaces to the case of unconditional Schauder decompositions in 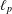 $\ell _{p}$ spaces. We also sharpen a stability theorem of Vizitei [‘On the stability of bases of subspaces in a Banach space’, in: Studies on Algebra and Mathematical Analysis, Moldova Academy of Sciences (Kartja Moldovenjaska, Chişinău, 1965), 32–44; (in Russian)] in the case of unconditional Schauder decompositions in any Banach space.
$\ell _{p}$ spaces. We also sharpen a stability theorem of Vizitei [‘On the stability of bases of subspaces in a Banach space’, in: Studies on Algebra and Mathematical Analysis, Moldova Academy of Sciences (Kartja Moldovenjaska, Chişinău, 1965), 32–44; (in Russian)] in the case of unconditional Schauder decompositions in any Banach space.