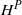 $H^P$
$H^P$Published online by Cambridge University Press: 01 August 2012
In this paper we consider the statistical concept of causality in continuous time between filtered probability spaces, based on Granger’s definitions of causality. Then we consider some stable subspaces of 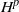 $H^p$ which contain right continuous modifications of martingales
$H^p$ which contain right continuous modifications of martingales 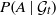 $P(A \mid {\mathcal {G}}_t)$. We give necessary and sufficient conditions, in terms of statistical causality, for these spaces to coincide with
$P(A \mid {\mathcal {G}}_t)$. We give necessary and sufficient conditions, in terms of statistical causality, for these spaces to coincide with 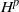 $H^p$. These results can be applied to extremal measures and regular weak solutions of stochastic differential equations.
$H^p$. These results can be applied to extremal measures and regular weak solutions of stochastic differential equations.