Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-26T14:48:30.625Z Has data issue: false hasContentIssue false
  • English
  • Français

STRICHARTZ ESTIMATES FOR THE WAVE EQUATION INSIDE CYLINDRICAL CONVEX DOMAINS

Part of: Hyperbolic equations and systems Harmonic analysis in several variables

Published online by Cambridge University Press:  08 August 2022

LEN MEAS Open the ORCID record for LEN MEAS [Opens in a new window]
LEN MEAS*
Affiliation:
Department of Mathematics, Royal University of Phnom Penh, Phnom Penh, Cambodia
*
e-mail: meas.len@rupp.edu.kh
Get access Rights & Permissions [Opens in a new window]

Abstract

We establish local-in-time Strichartz estimates for solutions of the model case Dirichlet wave equation inside cylindrical convex domains 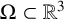$\Omega \subset \mathbb {R}^ 3$ with smooth boundary 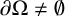$\partial \Omega \neq \emptyset $ . The key ingredients to prove Strichartz estimates are dispersive estimates, energy estimates, interpolation and 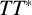$TT^*$ arguments. Strichartz estimates for waves inside an arbitrary domain $\Omega $ have been proved by Blair, Smith and Sogge [‘Strichartz estimates for the wave equation on manifolds with boundary’, Ann. Inst. H. Poincaré Anal. Non Linéaire 26 (2009), 1817–1829]. We provide a detailed proof of the usual Strichartz estimates from dispersive estimates inside cylindrical convex domains for a certain range of the wave admissibility.

Keywords

dispersive estimatesStrichartz estimateswave equationcylindrical convex domain

MSC classification

Primary: 35L05: Wave equation
Secondary: 42B25: Maximal functions, Littlewood-Paley theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 107 , Issue 2 , April 2023 , pp. 304 - 312
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bahouri, H., Chemin, J. Y. and Danchin, R., Fourier Analysis and Nonlinear Partial Differential Equations, Grundlehren der mathematischen Wissenschaften, 343 (Springer, Berlin–Heidelberg, 2011).CrossRefGoogle Scholar
Blair, M. D., Ford, G. A., Herr, S. and Marzuola, J. L., ‘Strichartz estimates for the Schrödinger equation on polygonal domains’, J. Geom. Anal. 22(2) (2012), 339–351.10.1007/s12220-010-9187-3CrossRefGoogle Scholar
Blair, M. D., Ford, G. A. and Marzuola, J. L., ‘Strichartz estimates for the wave equation on flat cones’, Int. Math. Res. Not. IMRN 3 (2013), 562–591.CrossRefGoogle Scholar
Blair, M. D., Smith, H. F. and Sogge, C. D., ‘Strichartz estimates for the wave equation on manifolds with boundary’, Ann. Inst. H. Poincaré Anal. Non Linéaire 26 (2009), 1817–1829.10.1016/j.anihpc.2008.12.004CrossRefGoogle Scholar
Brener, P., ‘On ${L}_p-{L}_{p^{\prime }}$ estimates for the wave equation’, Math. Z. 145 (1975), 251–254.Google Scholar
Burq, N., Lebeau, G. and Planchon, F., ‘Global existence for energy critical waves in 3-D domains’, J. Amer. Math. Soc. 21(3) (2008), 831–845.CrossRefGoogle Scholar
Ginibre, J. and Velo, G., ‘Smoothing properties and retarded estimates for some dispersive evolution equations’, Comm. Math. Phys. 144(1) (1992), 163–188.10.1007/BF02099195CrossRefGoogle Scholar
Ginibre, J. and Velo, G., ‘Generalized Strichartz inequalities for the wave equation’, J. Funct. Anal. 133 (1995), 749–774.CrossRefGoogle Scholar
Hörmander, L., The Analysis of Linear Partial Differential Operators I: Distribution Theory and Fourier Analysis, Classics in Mathematics (Springer-Verlag, New York, 2003).CrossRefGoogle Scholar
Ivanovici, O., Lebeau, G. and Planchon, F., ‘Dispersion for the wave equation inside strictly convex domains I: the Friedlander model case’, Ann. of Math. (2) 180 (2014), 323–380.CrossRefGoogle Scholar
Ivanovici, O., Lebeau, G. and Planchon, F., ‘Strichartz estimates for the wave equation on a 2D model convex domain’, J. Differential Equations 300 (2021), 830–880.CrossRefGoogle Scholar
Ivanovici, O. and Planchon, F., ‘Square function and heat flow estimates on domains’, Comm. Partial Differential Equations 42 (2017), 1447–1466.CrossRefGoogle Scholar
Meas, L., ‘Dispersive estimates for the wave equation inside cylindrical convex domains: a model case’, C. R. Math. Acad. Sci. Paris 355(2) (2017), 161–165.CrossRefGoogle Scholar
Meas, L., ‘Precise dispersive estimates for the wave equation inside cylindrical convex domains’, Proc. Amer. Math. Soc. 150(8) (2022), 3431–3443.Google Scholar