Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-11T01:14:12.110Z Has data issue: false hasContentIssue false
  • English
  • Français

STRICTLY POSITIVE SOLUTIONS FOR ONE-DIMENSIONAL NONLINEAR PROBLEMS INVOLVING THE 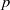$p$-LAPLACIAN

Part of: Elliptic equations and systems Boundary value problems

Published online by Cambridge University Press:  06 September 2013

U. KAUFMANN  and
I. MEDRI
U. KAUFMANN*
Affiliation:
FaMAF, Universidad Nacional de Córdoba, (5000) Córdoba, Argentina
I. MEDRI
Affiliation:
FaMAF, Universidad Nacional de Córdoba, (5000) Córdoba, Argentina email medri@mate.uncor.edu
*
✉kaufmann@mate.uncor.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 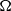$\Omega $ be a bounded open interval, and let 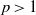$p\gt 1$ and 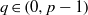$q\in (0, p- 1)$. Let 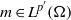$m\in {L}^{{p}^{\prime } } (\Omega )$ and 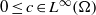$0\leq c\in {L}^{\infty } (\Omega )$. We study the existence of strictly positive solutions for elliptic problems of the form 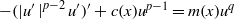$- (\vert {u}^{\prime } \mathop{\vert }\nolimits ^{p- 2} {u}^{\prime } ){\text{} }^{\prime } + c(x){u}^{p- 1} = m(x){u}^{q} $ in 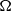$\Omega $, 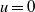$u= 0$ on 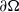$\partial \Omega $. We mention that our results are new even in the case 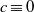$c\equiv 0$.

Keywords

elliptic one-dimensional problemsindefinite nonlinearitiesp-Laplacianstrictly positive solutions

MSC classification

Secondary: 34B15: Nonlinear boundary value problems 34B18: Positive solutions of nonlinear boundary value problems 35J25: Boundary value problems for second-order elliptic equations 35J61: Semilinear elliptic equations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 89 , Issue 2 , April 2014 , pp. 243 - 251
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Boccardo, L. and Orsina, L., ‘Sublinear equations in ${L}^{s} $’, Houston J. Math. 20 (1994), 99–114.Google Scholar
Chaparova, J. and Kutev, N., ‘Positive solutions of the generalized Emden–Fowler equation in Hölder spaces’, J. Math. Anal. Appl. 352 (2009), 65–76.CrossRefGoogle Scholar
Cuesta, M. and Ramos Quoirin, H., ‘A weighted eigenvalue problem for the $p$-Laplacian plus a potential’, NoDEA Nonlinear Differential Equations Appl. 16 (2009), 469–491.CrossRefGoogle Scholar
Díaz, J., Hernández, J. and Mancebo, F., ‘Branches of positive and free boundary solutions for some singular quasilinear elliptic problems’, J. Math. Anal. Appl. 352 (2009), 449–474.CrossRefGoogle Scholar
Drábek, P. and Hernández, J., ‘Existence and uniqueness of positive solutions for some quasilinear elliptic problems’, Nonlinear Anal. 44 (2001), 189–204.CrossRefGoogle Scholar
Du, Y., Order Structure and Topological Methods in Nonlinear Partial Differential Equations. Vol. 1. Maximum Principles and Applications, Series in Partial Differential Equations and Applications, 2 (World Scientific Publishing Co Ltd, Hackensack, NJ, 2006).Google Scholar
García-Melián, J. and Sabina de Lis, J., ‘Maximum and comparison principles for operators involving the $p$-Laplacian’, J. Math. Anal. Appl. 218 (1998), 49–65.CrossRefGoogle Scholar
Gasiński, L. and Papageorgiou, N., Nonlinear Analysis, Series in Mathematical Analysis and Applications, 9 (Chapman & Hall, Boca Raton, FL, 2006).Google Scholar
Godoy, T. and Kaufmann, U., ‘On strictly positive solutions for some semilinear elliptic problems’, NoDEA Nonlinear Differential Equations Appl. 20 (2013), 779–795.CrossRefGoogle Scholar
Manásevich, R. and Mawhin, J., ‘Periodic solutions for nonlinear systems with $p$-Laplacian-like operators’, J. Differential Equations 145 (1998), 367–393.Google Scholar
Manásevich, R. and Mawhin, J., ‘Boundary value problems for nonlinear perturbations of vector $p$-Laplacian-like operators’, J. Korean Math. Soc. 37 (2000), 665–685.Google Scholar