Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T10:03:18.534Z Has data issue: false hasContentIssue false
  • English
  • Français

A strong excision theorem for generalised Tate cohomology

Published online by Cambridge University Press:  17 April 2009

N. Mramor Kosta
N. Mramor Kosta
Affiliation:
Institute for Mathematics, Physics, Mechanics, Faculty of Computer and Information Science, University of Ljubljana, Slovenia, e-mail: neza.mramor-kosta@fri.uni-lj.si
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the analogue of the fixed point theorem of A. Borel in the context of Tate cohomology. We show that for general compact Lie groups G the Tate cohomology of a G-CW complex X with coefficients in a field of characteristic 0 is in general not isomorphic to the cohomology of the fixed point set, and thus the fixed point theorem does not apply. Instead, the following excision theorem is valid: if X′ is the subcomplex of all G-cells of orbit type G/H where dim H > 0, and V is a ring such that for every finite isotropy group H the order |H| is invertible in V, then 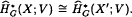. In the special cases G = 𝕋, the circle group, and G = 𝕌, the group of unit quaternions, a more elementary geometric proof, using a cellular model of 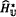is given.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 72 , Issue 1 , August 2005 , pp. 7 - 15
Copyright
Copyright © Australian Mathematical Society 2005

References

[1]Brown, K.S., Cohomology pf groups (Springer-Verlag, New York, 1982).CrossRefGoogle Scholar
[2]Cencelj, M., ‘Jones-Petrack cohomology’, Quart. J. Math. Oxford (2) 46 (1995), 409–415.Google Scholar
[3]Cencelj, M. and Kosta, N. Mramor, ‘CW decompositions of equivariant complexes’, Bull. Austr. Math. Soc. 65 (2002), 45–53.CrossRefGoogle Scholar
[4]Cencelj, M., Kosta, N. Mramor and Vavpetic, A., ‘G-complexes with a compatible CW structure’, J. Math. Kyoto Univ 43 (2003), 585–597.Google Scholar
[5]Goodwillie, T.G., ‘Cyclic homology, derivations, and the free loop space’, Topology 24 (1985), 187–215.Google Scholar
[6]Greenlees, J.P.C. and May, J.P., Generalized Tate cohomology, Memoirs of the American Mathematical Society 113 (American Mathematical Society, Providence, R.I., 1995).Google Scholar
[7]Hsiang, W.Y., Cohomology theory of topological transformation groups (Springer-Verlag, Berlin, Heidelberg, New York, 1975).Google Scholar
[8]Jones, J.D.S., ‘Cyclic homology and equivariant homology’, Invent. Math. 87 (1987), 403–423.Google Scholar
[9]Jones, J.D.S. and Petrack, S.B., ‘Le théorème des points fixes en cohomologie équivariante en dimension infinite’, C.R. Acad. Sci. Paris Ser.I 306 (1988), 75–78.Google Scholar
[10]Jones, J.D.S. and Petrack, S.B., ‘The fixed point theorem in equivariant cohomology’, Trans. Amer. Math. Soc. 322 (1990), 35–50.CrossRefGoogle Scholar
[11]Suzuki, I., Group theory I (Springer-Verlag, Berlin, Heidelberg, New York, 1982).Google Scholar
[12]torn Dieck, T., Transformation groups and representation theory, Lecture Notes in Mathematics 766 (Springer-Verlag, Berlin, Heidelberg, New York, 1979).CrossRefGoogle Scholar