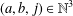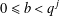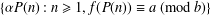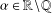Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wannes, Walid
2024.
On the frequency of the digits of the largest prime factor of an integer.
Boletín de la Sociedad Matemática Mexicana,
Vol. 30,
Issue. 3,
Wannes, Walid
and
Zouari, Hichem
2025.
The Level of Distribution of the Zeckendorf Sum-of-Digits Function over Friable Integers.
Vietnam Journal of Mathematics,
Wannes, Walid
and
Zouari, Hichem
2025.
On the friable mean value of additive arithmetic functions.
Acta Universitatis Sapientiae, Mathematica,
Vol. 17,
Issue. 1,