Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T18:13:20.310Z Has data issue: false hasContentIssue false
  • English
  • Français

SUBSETS OF VERTICES GIVE MORITA EQUIVALENCES OF LEAVITT PATH ALGEBRAS

Part of: Modules, bimodules and ideals

Published online by Cambridge University Press:  30 March 2017

LISA ORLOFF CLARK Open the ORCID record for LISA ORLOFF CLARK [Opens in a new window] ,
ASTRID AN HUEF Open the ORCID record for ASTRID AN HUEF [Opens in a new window]  and
PAREORANGA LUITEN-APIRANA
LISA ORLOFF CLARK
Affiliation:
Department of Mathematics and Statistics, University of Otago, PO Box 56, Dunedin 9054, New Zealand email lclark@maths.otago.ac.nz
ASTRID AN HUEF*
Affiliation:
Department of Mathematics and Statistics, University of Otago, PO Box 56, Dunedin 9054, New Zealand email astrid@maths.otago.ac.nz
PAREORANGA LUITEN-APIRANA
Affiliation:
Department of Mathematics and Statistics, University of Otago, PO Box 56, Dunedin 9054, New Zealand email pareorangaluitenapirana@gmail.com
*
✉astrid@maths.otago.ac.nz
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that every subset of vertices of a directed graph 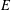$E$ gives a Morita equivalence between a subalgebra and an ideal of the associated Leavitt path algebra. We use this observation to prove an algebraic version of a theorem of Crisp and Gow: certain subgraphs of 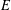$E$ can be contracted to a new graph 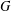$G$ such that the Leavitt path algebras of 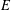$E$ and 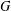$G$ are Morita equivalent. We provide examples to illustrate how desingularising a graph, and in- or out-delaying of a graph, all fit into this setting.

Keywords

directed graphLeavitt path algebraMorita contextMorita equivalencegraph algebra

MSC classification

Primary: 16D70: Structure and classification (except as in ), direct sum decomposition, cancellation
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 2 , October 2017 , pp. 212 - 222
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

This research has been supported by a University of Otago Research Grant.

References

Abrams, G. and Aranda Pino, G., ‘The Leavitt path algebras of arbitrary graphs’, Houston J. Math. 34 (2008), 423–442.Google Scholar
Abrams, G., Louly, A., Pardo, E. and Smith, C., ‘Flow invariants in the classification of Leavitt path algebras’, J. Algebra 333 (2011), 202–231.CrossRefGoogle Scholar
Aranda Pino, G., Martín Barquero, D., Martín González, C. and Siles Molina, M., ‘The socle of a Leavitt path algebra’, J. Pure Appl. Algebra 212 (2008), 500–509.CrossRefGoogle Scholar
Arklint, S., Gabe, J. and Ruiz, E., ‘Hereditary $C^{\ast }$ -subalgebras of graph algebras’, Preprint, 2016, arXiv:1604.03085.Google Scholar
Bates, T., ‘Applications of the gauge-invariant uniqueness theorem for graph algebras’, Bull. Aust. Math. Soc. 66 (2002), 57–67.CrossRefGoogle Scholar
Bates, T. and Pask, D., ‘Flow equivalence of graph algebras’, Ergodic Theory Dynam. Systems 24 (2004), 367–382.CrossRefGoogle Scholar
Clark, L. O., Flynn, C. and an Huef, A., ‘Kumjian–Pask algebras of locally convex higher-rank graphs’, J. Algebra 399 (2014), 445–474.CrossRefGoogle Scholar
Clark, L. O. and Pangalela, Y. E. P., ‘Kumjian–Pask algebras of finitely-aligned higher-rank graphs’, Preprint, 2016, arXiv:1512.06547.CrossRefGoogle Scholar
Clark, L. O. and Sims, A., ‘Equivalent groupoids have Morita equivalent Steinberg algebras’, J. Pure Appl. Algebra 219 (2015), 2062–2075.CrossRefGoogle Scholar
Crisp, T., ‘Corners of graph algebras’, J. Operator Theory 60 (2008), 253–271.Google Scholar
Crisp, T. and Gow, D., ‘Contractible subgraphs and Morita equivalence of graph C ∗ -algebras’, Proc. Amer. Math. Soc. 134 (2006), 2003–2013.CrossRefGoogle Scholar
Drinen, D. and Sieben, N., ‘ C ∗ -equivalences of graphs’, J. Operator Theory 45 (2001), 209–229.Google Scholar
Drinen, D. and Tomforde, M., ‘The C ∗ -algebras of arbitrary graphs’, Rocky Mountain J. Math. 35 (2005), 105–135.CrossRefGoogle Scholar
Johansen, R. and Sørensen, A. P. W., ‘The Cuntz splice does not preserve ∗-isomorphism of Leavitt path algebras over ℤ’, J. Pure Appl. Algebra 220 (2016), 3966–3983.CrossRefGoogle Scholar
Nasr-Isfahani, A. R., ‘Singular equivalence of finite dimensional algebras with radical square zero’, J. Pure Appl. Algebra 220 (2016), 3948–3965.CrossRefGoogle Scholar
Raeburn, I., Graph Algebras, CBMS Regional Conference Series in Mathematics, 103 (American Mathematical Society, Providence, RI, 2005).CrossRefGoogle Scholar
Sørensen, A. P. W., ‘Geometric classification of simple graph algebras’, Ergodic Theory Dynam. Systems 33 (2013), 1199–1220.CrossRefGoogle Scholar
Tomforde, M., ‘Leavitt path algebras with coefficients in a commutative ring’, J. Pure Appl. Algebra 215 (2011), 471–484.CrossRefGoogle Scholar