Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T12:00:24.614Z Has data issue: false hasContentIssue false
  • English
  • Français

SUBSPACES OF THE FREE TOPOLOGICAL VECTOR SPACE ON THE UNIT INTERVAL

Part of: Fairly general properties Generalities Topological linear spaces and related structures

Published online by Cambridge University Press:  07 August 2017

SAAK S. GABRIYELYAN  and
SIDNEY A. MORRIS Open the ORCID record for SIDNEY A. MORRIS [Opens in a new window]
SAAK S. GABRIYELYAN
Affiliation:
Department of Mathematics, Ben-Gurion University of the Negev, Beer-Sheva PO 653, Israel email saak@math.bgu.ac.il
SIDNEY A. MORRIS*
Affiliation:
Faculty of Science and Technology, Federation University Australia, PO Box 663, Ballarat, Victoria 3353, Australia Department of Mathematics and Statistics, La Trobe University, Melbourne, Victoria 3086, Australia email morris.sidney@gmail.com
*
✉morris.sidney@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a Tychonoff space 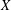$X$, let 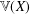$\mathbb{V}(X)$ be the free topological vector space over 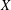$X$, 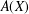$A(X)$ the free abelian topological group over 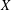$X$ and 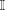$\mathbb{I}$ the unit interval with its usual topology. It is proved here that if 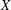$X$ is a subspace of 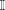$\mathbb{I}$, then the following are equivalent: 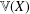$\mathbb{V}(X)$ can be embedded in 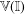$\mathbb{V}(\mathbb{I})$ as a topological vector subspace; 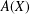$A(X)$ can be embedded in 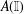$A(\mathbb{I})$ as a topological subgroup; 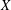$X$ is locally compact.

Keywords

free topological vector spacefree topological groupfree abelian topological groupembeddinglocally compact

MSC classification

Primary: 46A03: General theory of locally convex spaces
Secondary: 54A25: Cardinality properties (cardinal functions and inequalities, discrete subsets) 54D50: $k$-spaces
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 1 , February 2018 , pp. 110 - 118
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Engelking, R., General Topology (Panstwowe Wydawnictwo Naukowe, Waszawa, 1977).Google Scholar
Gabriyelyan, S. S. and Morris, S. A., ‘Free topological vector spaces’, Topology Appl. 223 (2017), 30–49.Google Scholar
Gabriyelyan, S. S. and Morris, S. A., ‘Embedding into free topological vector spaces on compact metrizable spaces’. Preprint.Google Scholar
Katz, E., Morris, S. A. and Nickolas, P., ‘A free subgroup of the free abelian topological group on the unit interval’, Bull. Lond. Math. Soc. 14 (1982), 399–402.Google Scholar
Mack, J., Morris, S. A. and Ordman, E. T., ‘Free topological groups and the projective dimension of a locally compact abelian groups’, Proc. Amer. Math. Soc. 40 (1973), 303–308.Google Scholar
Tkachenko, M. G., ‘On completeness of free abelian topological groups’, Soviet Math. Dokl. 27 (1983), 341–345.Google Scholar