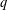Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bachraoui, Mohamed El
2022.
Some new q-series identities through an extended Bailey transform.
The Ramanujan Journal,
Vol. 58,
Issue. 3,
p.
747.