Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-11T08:13:27.641Z Has data issue: false hasContentIssue false
  • English
  • Français

SUMSETS AND DIFFERENCE SETS CONTAINING A COMMON TERM OF A SEQUENCE

Part of: Sequences and sets Extremal combinatorics

Published online by Cambridge University Press:  26 September 2011

QUAN-HUI YANG  and
YONG-GAO CHEN
QUAN-HUI YANG
Affiliation:
School of Mathematical Sciences and Institute of Mathematics, Nanjing Normal University, Nanjing 210046, PR China
YONG-GAO CHEN*
Affiliation:
School of Mathematical Sciences and Institute of Mathematics, Nanjing Normal University, Nanjing 210046, PR China (email: ygchen@njnu.edu.cn)
*
✉For correspondence; e-mail: ygchen@njnu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let β>1 be a real number, and let {ak} be an unbounded sequence of positive integers such that ak+1/ak≤β for all k≥1. The following result is proved: if n is an integer with n>(1+1/(2β))a1 and A is a subset of {0,1,…,n} with 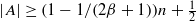, then (A+A)∩(A−A) contains a term of {ak }. The lower bound for |A| is optimal. Beyond these, we also prove that if n≥3 is an integer and A is a subset of {0,1,…,n} with 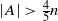, then (A+A)∩(A−A) contains a power of 2. Furthermore, cannot be improved.

Keywords

sumsetsdifference setssequences

MSC classification

Secondary: 11B13: Additive bases, including sumsets 05D05: Extremal set theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 85 , Issue 1 , February 2012 , pp. 79 - 83
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2011

Footnotes

This work was supported by the National Natural Science Foundation of China, Grant No. 11071121.

References

[1]Abe, T., ‘Sumsets containing powers of an integer’, Combinatorica 24 (2004), 1–4.CrossRefGoogle Scholar
[2]Alon, N., ‘Subset sums’, J. Number Theory 27 (1987), 196–205.CrossRefGoogle Scholar
[3]Erdős, P. and Freiman, G., ‘On two additive problems’, J. Number Theory 34 (1990), 1–12.CrossRefGoogle Scholar
[4]Freiman, G. A., ‘Sumsets and powers of 2’, Colloq. Math. Soc. János Bolyai 60 (1992), 279–286.Google Scholar
[5]Kapoor, V., ‘Sets whose sumset avoids a thin sequence’, J. Number Theory 130 (2010), 534–538.CrossRefGoogle Scholar
[6]Lev, V. F., ‘Representing powers of 2 by a sum of four integers’, Combinatorica 16 (1996), 413–416.CrossRefGoogle Scholar
[7]Nathanson, M. B. and Sárközy, A., ‘Sumsets containing long arithmetic progressions and powers of 2’, Acta Arith. 54 (1989), 147–154.CrossRefGoogle Scholar
[8]Pan, H., ‘Note on integer powers in sumsets’, J. Number Theory 117 (2006), 216–221.CrossRefGoogle Scholar