Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-29T04:26:47.706Z Has data issue: false hasContentIssue false
  • English
  • Français

SYMMETRIC ITINERARY SETS: ALGORITHMS AND NONLINEAR EXAMPLES

Part of: Classical measure theory Communication, information Low-dimensional dynamical systems

Published online by Cambridge University Press:  20 March 2019

BRENDAN HARDING Open the ORCID record for BRENDAN HARDING [Opens in a new window]
BRENDAN HARDING*
Affiliation:
School of Mathematical Sciences, The University of Adelaide, Adelaide, South Australia 5005, Australia email brendan.harding@adelaide.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We describe how to approximate fractal transformations generated by a one-parameter family of dynamical systems 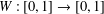$W:[0,1]\rightarrow [0,1]$ constructed from a pair of monotone increasing diffeomorphisms 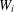$W_{i}$ such that 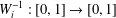$W_{i}^{-1}:[0,1]\rightarrow [0,1]$ for 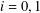$i=0,1$. An algorithm is provided for determining the unique parameter value such that the closure of the symbolic attractor 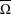$\overline{\unicode[STIX]{x1D6FA}}$ is symmetrical. Several examples are given, one in which the 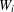$W_{i}$ are affine and two in which the 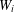$W_{i}$ are nonlinear. Applications to digital imaging are also discussed.

Keywords

expanding dynamical systemfractal transformationchaos game algorithm

MSC classification

Primary: 37E05: Maps of the interval (piecewise continuous, continuous, smooth)
Secondary: 28A80: Fractals 94A08: Image processing (compression, reconstruction, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 1 , August 2019 , pp. 109 - 118
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

The author acknowledges support from an Australian Research Council Discovery Project (project number DP160102021) funded by the Australian Government.

References

Barnsley, M. F., Fractals Everywhere, 2nd edn (Academic Press, London, 1993).Google Scholar
Barnsley, M. F., Harding, B. and Igudesman, K., ‘How to transform and filter images using iterated function systems’, SIAM J. Imaging Sci. 4(4) (2011), 1001–1028.Google Scholar
Barnsley, M. F. and Mihalache, N., ‘Symmetric itinerary sets’, Bull. Aust. Math. Soc., to appear.Google Scholar
Hoggar, S. G. and Mcfarlane, I., ‘Faster fractal pictures by finite fields and far rings’, Discrete Math. 138(1) (1995), 267–280.Google Scholar
McFarlane, I. and Hoggar, S. G., ‘Optimal drivers for the ‘random’ iteration algorithm’, Comput. J. 37(7) (1994), 629–640.Google Scholar
Mendivil, F., ‘Fractals, graphs, and fields’, Amer. Math. Monthly 110(6) (2003), 503–515.Google Scholar
Ruskey, F., Savage, C. and Wang, T. M. Y., ‘Generating necklaces’, J. Algorithms 13(3) (1992), 414–430.Google Scholar
Osher, S. and Fedkiw, R., ‘Signed distance functions’, in: Level Set Methods and Dynamic Implicit Surfaces (eds. Osher, S. and Fedkiw, R.) (Springer, New York, 2003), 17–22.Google Scholar