No CrossRef data available.
Article contents
SYSTEMS OF CONGRUENCES WITH PRODUCTS OF VARIABLES FROM SHORT INTERVALS
Published online by Cambridge University Press: 11 November 2015
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We obtain an upper bound for the number of solutions to the system of 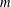 $m$ congruences of the type modulo a prime
$m$ congruences of the type modulo a prime 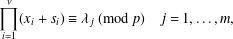 $$\begin{eqnarray}\displaystyle \mathop{\prod }_{i=1}^{{\it\nu}}(x_{i}+s_{i})\equiv {\it\lambda}_{j}~(\text{mod }p)\quad j=1,\ldots ,m, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\prod }_{i=1}^{{\it\nu}}(x_{i}+s_{i})\equiv {\it\lambda}_{j}~(\text{mod }p)\quad j=1,\ldots ,m, & & \displaystyle \nonumber\end{eqnarray}$$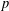 $p$, with variables
$p$, with variables 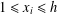 $1\leq x_{i}\leq h$,
$1\leq x_{i}\leq h$, 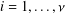 $i=1,\ldots ,{\it\nu}$ and arbitrary integers
$i=1,\ldots ,{\it\nu}$ and arbitrary integers 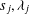 $s_{j},{\it\lambda}_{j}$,
$s_{j},{\it\lambda}_{j}$, 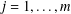 $j=1,\ldots ,m$, for a parameter
$j=1,\ldots ,m$, for a parameter 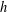 $h$ significantly smaller than
$h$ significantly smaller than 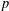 $p$. We also mention some applications of this bound.
$p$. We also mention some applications of this bound.
MSC classification
Primary:
11D79: Congruences in many variables
Secondary:
11L40: Estimates on character sums
Information
- Type
- Research Article
- Information
- Copyright
- © 2015 Australian Mathematical Publishing Association Inc.
References
Ahlswede, R., Mauduit, C. and Sárközy, A., ‘Large families of pseudorandom sequences of k symbols and their complexity I’, in: General Theory of Information Transfer and Combinatorics, Lecture Notes in Computer Science, 4123 (Springer, Berlin, 2006), 293–307.CrossRefGoogle Scholar
Ayyad, A., Cochrane, T. and Zheng, Z., ‘The congruence x 1x 2 ≡ x 3x 4 (modp), the equation x 1x 2 = x 3x 4 and the mean values of character sums’, J. Number Theory 59 (1996), 398–413.Google Scholar
Bourgain, J. and Garaev, M. Z., ‘Sumsets of reciprocals in prime fields and multilinear Kloosterman sums’, Izv. Math. 78 (2014), 656–707.Google Scholar
Bourgain, J., Garaev, M. Z., Konyagin, S. V. and Shparlinski, I. E., ‘On the hidden shifted power problem’, SIAM J. Comput. 41 (2012), 1524–1557.Google Scholar
Bourgain, J., Garaev, M. Z., Konyagin, S. V. and Shparlinski, and I. E., ‘On congruences with products of variables from short intervals and applications’, Proc. Steklov Inst. Math. 280 (2013), 67–96.Google Scholar
Bourgain, J., Garaev, M. Z., Konyagin, S. V. and Shparlinski, and I. E., ‘Multiplicative congruences with variables from short intervals’, J. d’Anal. Math. 124 (2014), 117–147.Google Scholar
Gómez-Pérez, D., Gutierrez, J., Ibeas, A. and Sevilla, D., ‘Common factors of resultants modulo p’, Bull. Aust. Math. Soc. 79 (2009), 299–302.Google Scholar
Gómez-Pérez, D. and Shparlinski, I. E., ‘Subgroups generated by rational functions in finite fields’, Monatsh. Math. 176 (2015), 241–253.Google Scholar
Hubert, P., Mauduit, C. and Sárközy, A., ‘On pseudorandom binary lattices’, Acta Arith. 125 (2006), 51–62.Google Scholar
Ivanyos, G., Karpinski, M., Santha, M., Saxena, N. and Shparlinski, and I. E., ‘Polynomial interpolation and identity testing from high powers over finite fields’, Preprint, 2015, arXiv:1502.06631.Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory (American Mathematical Society, Providence, RI, 2004).Google Scholar
Konyagin, S. V. and Shparlinski, I. E., Character Sums with Exponential Functions and Their Applications (Cambridge University Press, Cambridge, 1999).Google Scholar
Lamzouri, Y., ‘The distribution of short character sums’, Math. Proc. Cambridge Philos. Soc. 155 (2013), 207–218.Google Scholar
Mérai, L., ‘Construction of pseudorandom binary lattices based on multiplicative characters’, Period. Math. Hungar. 59 (2009), 43–51.CrossRefGoogle Scholar
Shparlinski, I. E., ‘Polynomial values in small subgroups of finite fields’, Rev. Mat. Iberoam., to appear.Google Scholar
Tóth, V., ‘Extension of the notion of collision and avalanche effect to sequences of k symbols’, Period. Math. Hungar. 65 (2012), 229–238.Google Scholar

