Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T16:18:41.266Z Has data issue: false hasContentIssue false
  • English
  • Français

$\textit{h}$-MINIMUM SPANNING LENGTHS AND AN EXTENSION TO BURNSIDE’S THEOREM ON IRREDUCIBILITY

Part of: Basic linear algebra

Published online by Cambridge University Press:  02 December 2020

W. E. LONGSTAFF Open the ORCID record for W. E. LONGSTAFF [Opens in a new window]
W. E. LONGSTAFF*
Affiliation:
11 Tussock Crescent, Elanora, Queensland4221, Australia e-mail: bill.longstaff@alumni.utoronto.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

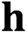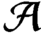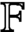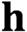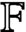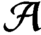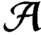We introduce the $\textbf{h}$ -minimum spanning length of a family ${\mathcal A}$ of $n\times n$ matrices over a field $\mathbb F$ , where $\textbf{h}$ is a p-tuple of positive integers, each no more than n. For an algebraically closed field $\mathbb F$ , Burnside’s theorem on irreducibility is essentially that the $(n,n,\ldots ,n)$ -minimum spanning length of ${\mathcal A}$ exists if ${\mathcal A}$ is irreducible. 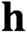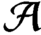We show that the $\textbf{h}$ -minimum spanning length of ${\mathcal A}$ exists for every 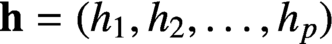$\textbf{h}=(h_1,h_2,\ldots , h_p)$ if 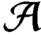${\mathcal A}$ is an irreducible family of invertible matrices with at least three elements. The $(1,1, \ldots ,1)$ -minimum spanning length is at most 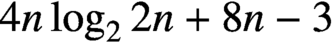$4n\log _{2} 2n+8n-3$ . Several examples are given, including one giving a complete calculation of the 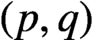$(p,q)$ -minimum spanning length of the ordered pair 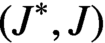$(J^*,J)$ , where J is the Jordan matrix.

Keywords

irreduciblelinear span

MSC classification

Primary: 15A30: Algebraic systems of matrices
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 104 , Issue 1 , August 2021 , pp. 78 - 93
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Guterman, A. E., Laffey, T., Markova, O. V. and Šmigoc, H., ‘A resolution of Paz’s conjecture in the presence of a nonderogatory matrix’, Linear Algebra Appl. 543 (2018), 234–250.CrossRefGoogle Scholar
Halmos, P. R., Finite-Dimensional Vector Spaces, Undergraduate Texts in Mathematics, 2nd edn, reprint (Springer, New York, 1974).CrossRefGoogle Scholar
Laffey, T., Markova, O. V. and Šmigoc, H., ‘The effect of assuming the identity as a generator on the length of the matrix algebra’, Linear Algebra Appl. 498 (2016), 378–393.CrossRefGoogle Scholar
Lambrou, M. S. and Longstaff, W. E., ‘On the lengths of pairs of complex matrices of size six’, Bull. Aust. Math. Soc. 80 (2009), 177–201.CrossRefGoogle Scholar
Lomonosov, V. and Rosenthal, P., ‘The simplest proof of Burnside’s theorem on matrix algebras’, Linear Algebra Appl. 383 (2004), 45–47.CrossRefGoogle Scholar
Longstaff, W. E., ‘Burnside’s theorem: irreducible pairs of transformations’, Linear Algebra Appl. 382 (2004), 247–269.CrossRefGoogle Scholar
Longstaff, W. E., ‘Irreducible families of complex matrices containing a rank one matrix’, Bull. Aust. Math. Soc. 102(2) (2020), 226–236.CrossRefGoogle Scholar
Longstaff, W. E., ‘The slot length of a family of matrices’, Bull. Aust. Math. Soc., to appear.Google Scholar
Longstaff, W. E., Niemeyer, A. C. and Panaia, O., ‘On the length of pairs of complex matrices of size at most five’, Bull. Aust. Math. Soc. 73 (2006), 461–472.CrossRefGoogle Scholar
Longstaff, W. E. and Rosenthal, P., ‘On the lengths of irreducible pairs of complex matrices’, Proc. Amer. Math. Soc. 139(11) (2011), 3769–3777.CrossRefGoogle Scholar
Paz, A., ‘An application of the Cayley–Hamilton theorem to matrix polynomials in several variables’, Linear Multilinear Algebra A 15 (1984), 161–170.CrossRefGoogle Scholar
Shitov, Y., ‘An improved bound for the lengths of matrix algebras’ (English summary), Algebra Number Theory 13(6) (2019), 1501–1507.CrossRefGoogle Scholar