Hostname: page-component-76c49bb84f-t7r7g Total loading time: 0 Render date: 2025-07-09T17:06:29.719Z Has data issue: false hasContentIssue false
  • English
  • Français

THREE ALGORITHMIC APPROACHES TO THE GENERAL POSITION PROBLEM

Part of: Graph theory

Published online by Cambridge University Press:  04 July 2025

ZAHRA HAMED-LABBAFIAN Open the ORCID record for ZAHRA HAMED-LABBAFIAN [Opens in a new window] ,
NARJES SABEGHI Open the ORCID record for NARJES SABEGHI [Opens in a new window] ,
MOSTAFA TAVAKOLI Open the ORCID record for MOSTAFA TAVAKOLI [Opens in a new window]  and
SANDI KLAVŽAR Open the ORCID record for SANDI KLAVŽAR [Opens in a new window]
ZAHRA HAMED-LABBAFIAN
Affiliation:
Department of Applied Mathematics, Faculty of Mathematical Sciences, https://ror.org/00g6ka752 Ferdowsi University of Mashhad , Mashhad, Iran e-mail: hamedlabbafianzahra@gmail.com
NARJES SABEGHI*
Affiliation:
Department of Mathematics, Faculty of Basic Sciences, Velayat University, Iranshar, Iran
MOSTAFA TAVAKOLI
Affiliation:
Department of Applied Mathematics, Faculty of Mathematical Sciences, https://ror.org/00g6ka752 Ferdowsi University of Mashhad , Mashhad, Iran e-mail: m_tavakoli@um.ac.ir
SANDI KLAVŽAR
Affiliation:
Faculty of Mathematics and Physics, https://ror.org/01d5jce07 University of Ljubljana , Ljubljana, Slovenia; Institute of Mathematics, Physics and Mechanics, Ljubljana, Slovenia; and Faculty of Natural Sciences and Mathematics, University of Maribor, Maribor, Slovenia e-mail: sandi.klavzar@fmf.uni-lj.si
*
e-mail: n.sabeghi@velayat.ac.ir
Get access Rights & Permissions [Opens in a new window]

Abstract

If G is a graph, then 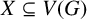$X\subseteq V(G)$ is a general position set if for every two vertices 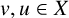$v,u\in X$ and every shortest 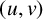$(u,v)$-path P, no inner vertex of P lies in X. We propose three algorithms to compute a largest general position set in G: an integer linear programming algorithm, a genetic algorithm and a simulated annealing algorithm. These approaches are supported by examples from different areas of graph theory.

Keywords

general position setgeneral position numberinteger linear programminggenetic algorithmsimulated annealing algorithm

MSC classification

Primary: 05C12: Distance in graphs
Secondary: 05C69: Dominating sets, independent sets, cliques 05C76: Graph operations (line graphs, products, etc.) 05C85: Graph algorithms

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 9
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Sandi Klavžar was supported by the Slovenian Research and Innovation Agency (ARIS) under the grants P1-0297, N1-0355 and N1-0285.

References

Araujo, J., Dourado, M. C., Protti, F. and Sampaio, R., ‘The iteration time and the general position number in graph convexities’, Appl. Math. Comput. 487 (2025), Article no. 129084.Google Scholar
Di Stefano, G., ‘Mutual visibility in graphs’, Appl. Math. Comput. 419 (2022), Article no. 126850.Google Scholar
Di Stefano, G., Klavžar, S., Krishnakumar, A., Tuite, J. and Yero, I. G., ‘Lower general position numbers in graphs’, Discuss. Math. Graph Theory 45 (2025), 509–531.10.7151/dmgt.2542CrossRefGoogle Scholar
Iršič, V., Klavžar, S., Rus, G. and Tuite, J., ‘General position polynomials’, Results Math. 79 (2024), Article no. 110.10.1007/s00025-024-02133-3CrossRefGoogle Scholar
Klavžar, S., Krishnakumar, A., Tuite, J. and Yero, I. G., ‘Traversing a graph in general position’, Bull. Aust. Math. Soc. 108 (2023), 1–13.10.1017/S0004972723000102CrossRefGoogle Scholar
Klavžar, S., Kuziak, D., Peterin, I. and Yero, I. G., ‘A Steiner general position problem in graph theory’, Comput. Appl. Math. 40 (2021), 1–15.10.1007/s40314-021-01619-yCrossRefGoogle Scholar
Körner, J., ‘On the extremal combinatorics of the Hamming space’, J. Combin. Theory Ser. A 71 (1995), 112–126.10.1016/0097-3165(95)90019-5CrossRefGoogle Scholar
Korže, D. and Vesel, A., ‘General position sets in two families of Cartesian product graphs’, Mediterr. J. Math. 20 (2023), Article no. 203.10.1007/s00009-023-02416-zCrossRefGoogle Scholar
Manuel, P. and Klavžar, S., ‘A general position problem in graph theory’, Bull. Aust. Math. Soc. 98 (2018) 177–187.10.1017/S0004972718000473CrossRefGoogle Scholar
Manuel, P., Prabha, R. and Klavžar, S., ‘The edge general position problem’, Bull. Malays. Math. Sci. Soc. 45 (2022), 2997–3009.10.1007/s40840-022-01319-8CrossRefGoogle Scholar
Melker, A. I. and Krupina, M. A., ‘Geometric modeling of midi-fullerene growth from ${C}_{32}$ to ${C}_{60}$ ’, St. Petersbg. State Polytech. Univ. J.: Phys. Math. 3 (2017), 22–28.Google Scholar
Thankachy, M., Ullas Chandran, S. V., Tuite, J., Thomas, E., Di Stefano, G. and Erskine, G., ‘On the vertex position number of graphs’, Discuss. Math. Graph Theory 44 (2024), 1169–1188.10.7151/dmgt.2491CrossRefGoogle Scholar
Thomas, E. J., Ullas Chandran, S. V., Tuite, J. and Di Stefano, G., ‘On monophonic position sets in graphs’, Discrete Appl. Math. 354 (2024), 72–82.10.1016/j.dam.2023.02.021CrossRefGoogle Scholar
Thomas, E. J., Ullas Chandran, S. V., Tuite, J. and Di Stefano, G., ‘On the general position number of Mycielskian graphs’, Discrete Appl. Math. 353 (2024), 29–43.10.1016/j.dam.2024.03.015CrossRefGoogle Scholar
Tian, J. and Klavžar, S., ‘Variety of general position problems in graphs’, Bull. Malays. Math. Sci. Soc. 48 (2025), Article no. 5.10.1007/s40840-024-01788-zCrossRefGoogle Scholar
Tian, J. and Xu, K., ‘On the general position number of the $k$ -th power graphs’, Quaest. Math. 47 (2024), 2215–2230.10.2989/16073606.2024.2352568CrossRefGoogle Scholar
Tuite, J., Thomas, E. and Ullas Chandran, S. V., ‘On some extremal position problems for graphs,’ Ars Math. Contemp. 25 (2025), Article no. P1.09.10.26493/1855-3974.3094.bc6CrossRefGoogle Scholar
Ullas Chandran, S. V. and Jaya Parthasarathy, G., ‘The geodesic irredundant sets in graphs’, Int. J. Math. Comb. 4 (2016), 135–143.Google Scholar
Ullas Chandran, S. V., Klavžar, S. and Tuite, J., ‘The general position problem: a survey’, Preprint, 2025, arXiv:2501.19385 [math.CO].Google Scholar