Article contents
TOEPLITZ OPERATORS BETWEEN FOCK SPACES
Published online by Cambridge University Press: 02 June 2015
Abstract
Given a positive Borel measure 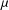 ${\it\mu}$ on the
${\it\mu}$ on the  $n$-dimensional Euclidean space
$n$-dimensional Euclidean space 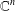 $\mathbb{C}^{n}$, we characterise the boundedness (and compactness) of Toeplitz operators
$\mathbb{C}^{n}$, we characterise the boundedness (and compactness) of Toeplitz operators 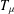 $T_{{\it\mu}}$ between Fock spaces
$T_{{\it\mu}}$ between Fock spaces 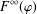 $F^{\infty }({\it\varphi})$ and
$F^{\infty }({\it\varphi})$ and 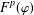 $F^{p}({\it\varphi})$ with
$F^{p}({\it\varphi})$ with 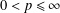 $0<p\leq \infty$ in terms of
$0<p\leq \infty$ in terms of  $t$-Berezin transforms and averaging functions of
$t$-Berezin transforms and averaging functions of 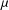 ${\it\mu}$. Our result extends recent work of Mengestie [‘On Toeplitz operators between Fock spaces’, Integral Equations Operator Theory78 (2014), 213–224] and others.
${\it\mu}$. Our result extends recent work of Mengestie [‘On Toeplitz operators between Fock spaces’, Integral Equations Operator Theory78 (2014), 213–224] and others.
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 92 , Issue 2 , October 2015 , pp. 316 - 324
- Copyright
- © 2015 Australian Mathematical Publishing Association Inc.
References
- 4
- Cited by


