Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-03-02T21:17:36.329Z Has data issue: false hasContentIssue false
  • English
  • Français

THE TOP LEFT DERIVED FUNCTORS OF THE GENERALISED 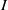$I$-ADIC COMPLETION

Part of: Homological methods Commutative algebra: Homological methods

Published online by Cambridge University Press:  04 January 2013

TRAN TUAN NAM
TRAN TUAN NAM*
Affiliation:
Department of Mathematics – Informatics, Ho Chi Minh University of Pedagogy, 280 An Duong Vuong, District 5, Ho Chi Minh City, Vietnam email namtuantran@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the top left derived functors of the generalised 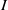$I$-adic completion and obtain equivalent properties concerning the vanishing or nonvanishing of the modules ${L}_{i} {\Lambda }_{I} (M, N)$. We also obtain some results for the sets 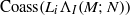$\text{Coass} ({L}_{i} {\Lambda }_{I} (M; N))$ and 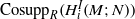${\text{Cosupp} }_{R} ({ H}_{i}^{I} (M; N))$.

Keywords

derived functorgeneralised I-adic completion(generalised) local homologyco-associated prime

MSC classification

Secondary: 13D45: Local cohomology 16E30: Homological functors on modules (Tor, Ext, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 2 , October 2013 , pp. 259 - 266
Copyright
Copyright ©2012 Australian Mathematical Publishing Association Inc. 

References

Bartijn, J., Flatness, Completions, Regular Sequences, un Ménage à Trois, Thesis, Utrecht, 1985.Google Scholar
Cuong, N. T. and Nam, T. T., ‘A local homology theory for linearly compact modules’, J. Algebra 319 (2008), 4712–4737.CrossRefGoogle Scholar
Cuong, N. T. and Nam, T. T., ‘The $I$-adic completion and local homology for Artinian modules’, Math. Proc. Cambridge Philos. Soc. 131 (2001), 61–72.CrossRefGoogle Scholar
Cuong, N. T. and Nam, T. T., ‘On the co-localization, co-support and co-associated primes of local homology modules’, Vietnam J. Math. 29 (4) (2001), 359–368.Google Scholar
Herzog, J., Komplexe, Auflösungen und Dualität in der localen Algebra (Habilitationsschrift Univ. Regensburg, 1970).Google Scholar
Kirby, D., ‘Dimension and length of artinian modules’, Quart. J. Math. Oxford 2 (41) (1990), 419–429.CrossRefGoogle Scholar
Macdonald, I. G., ‘Duality over complete local rings’, Topology 1 (1962), 213–235.CrossRefGoogle Scholar
Marley, T., ‘The associated primes of local cohomology modules over rings of small dimension’, Manuscripta Math. 104 (2001), 519–525.CrossRefGoogle Scholar
Melkersson, L. and Schenzel, P., ‘The co-localization of an Artinian module’, Proc. Edinb. Math. Soc. 38 (1995), 121–131.CrossRefGoogle Scholar
Nam, T. T., ‘Left derived functors od the generalized $I$-adic completion and generalized local homology’, Comm. Algebra 38 (2010), 440–453.CrossRefGoogle Scholar
Nam, T. T., ‘The finiteness of coassociated primes of generalized local homology modules’, Preprint.Google Scholar
Nam, T. T., ‘Generalized local homology and cohomology for artinian modules’, Algebra Colloquium 19 (1) (2012), 1205–1212.CrossRefGoogle Scholar
Nam, T. T., ‘Co-support and Coartinian modules’, Algebra Colloq. 15 (1) (2008), 83–96.CrossRefGoogle Scholar
Roberts, R. N., ‘Krull dimension for artinian modules over quasilocal commutative rings’, Quart. J. Math. Oxford 26 (3) (1975), 269–273.CrossRefGoogle Scholar
Rotman, J. J., An Introduction to Homological Algebra (Academic Press, 1979).Google Scholar
Sharp, R. Y., ‘A method for the study of artinian modules with an application to asymptotic behavior’, Commutative Algebra, Math. Sciences Research Inst. Publ., 15 (Springer, 1989), pp. 443–465.CrossRefGoogle Scholar
Yassemi, S., ‘Coassociated primes’, Comm. Algebra 23 (1995), 1473–1498.CrossRefGoogle Scholar
Zöschinger, H., ‘Linear-kompakte Moduln über noetherschen Ringen’, Arch. Math. 41 (1983), 121–130.CrossRefGoogle Scholar