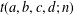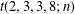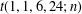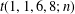Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ding, Yihao
Gu, Dieqi
Huang, Tinghao
Jiang, Qinghai
and
Ye, Dongxi
2022.
On Conjectures of Z.-H. Sun.
Results in Mathematics,
Vol. 77,
Issue. 3,