Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T06:09:00.479Z Has data issue: false hasContentIssue false
  • English
  • Français

THE TUMURA–CLUNIE THEOREM IN SEVERAL COMPLEX VARIABLES

Part of: Holomorphic mappings and correspondences Holomorphic functions of several complex variables

Published online by Cambridge University Press:  13 June 2014

PEI-CHU HU  and
CHUNG-CHUN YANG
PEI-CHU HU*
Affiliation:
School of Mathematics, Shandong University, Jinan 250100, Shandong, PR China email pchu@sdu.edu.cn
CHUNG-CHUN YANG
Affiliation:
College of Science, China University of Petroleum (Huadong), Qingdao 266580, Shandong, PR China email wood.yang@family.ust.hk
*
✉pchu@sdu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is a well-known result that if a nonconstant meromorphic function 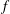$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}f$ on 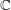$\mathbb{C}$ and its 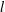$l$th derivative 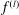$f^{(l)}$ have no zeros for some 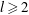$l\geq 2$, then 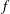$f$ is of the form 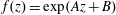$f(z)=\exp (Az+B)$ or 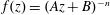$f(z)=(Az+B)^{-n}$ for some constants 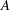$A$, 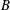$B$. We extend this result to meromorphic functions of several variables, by first extending the classic Tumura–Clunie theorem for meromorphic functions of one complex variable to that of meromorphic functions of several complex variables using Nevanlinna theory.

Keywords

meromorphic functionNevanlinna theoryTumura–Clunie theorem

MSC classification

Secondary: 32A15: Entire functions 32A20: Meromorphic functions 32A22: Nevanlinna theory (local); growth estimates; other inequalities 32H30: Value distribution theory in higher dimensions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 90 , Issue 3 , December 2014 , pp. 444 - 456
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Clunie, J., ‘On integral and meromorphic functions’, J. Lond. Math. Soc. 37 (1962), 17–27.CrossRefGoogle Scholar
Frank, G., ‘Eine Vermutung von Hayman über Nullstellen meromorpher Funktionen’, Math. Z. 149 (1976), 29–36.CrossRefGoogle Scholar
Frank, G., Hennekemper, W. and Polloczek, G., ‘Über die Nullstellen meromorpher Funktionen und ihrer Ableitungen’, Math. Ann. 225 (1977), 145–154.Google Scholar
Griffiths, Ph. and King, J., ‘Nevanlinna theory and holomorphic mappings between algebraic varieties’, Acta Math. 130 (1973), 145–220.Google Scholar
Hayman, W. K., ‘Picard values of meromorphic functions and their derivatives’, Ann. of Math. (2) 70 (1959), 9–42.Google Scholar
Hayman, W. K., Meromorphic Functions (Clarendon Press, Oxford, 1964).Google Scholar
Hu, P. C., Li, P. and Yang, C. C., Unicity of Meromorphic Mappings (Kluwer Academic Publishers, Dordrecht, 2003).Google Scholar
Hu, P. C. and Yang, C. C., ‘Malmquist type theorem and factorization of meromorphic solutions of partial differential equations’, Complex Var. 27 (1995), 269–285.Google Scholar
Langley, J. K., ‘Proof of a conjecture of Hayman concerning f and f ′ ′’, J. Lond. Math. Soc. (2) 48 (1993), 500–514.Google Scholar
Li, B. Q., ‘On reduction of functional-differential equations’, Complex Var. 31 (1996), 311–324.Google Scholar
Stoll, W., Value Distribution on Parabolic Spaces, Lecture Notes in Mathematics, 600 (Springer, Berlin, 1977).Google Scholar
Tumura, Y., ‘On the extensions of Borel’s theorem and Saxer-Csillag’s theorem’, Proc. Phys. Math. Soc. Jpn. (3) 19 (1937), 29–35.Google Scholar