Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T20:06:21.604Z Has data issue: false hasContentIssue false
  • English
  • Français

TWO NEW GENERALISED HYPERSTABILITY RESULTS FOR THE DRYGAS FUNCTIONAL EQUATION

Part of: Nonlinear operators and their properties

Published online by Cambridge University Press:  09 January 2017

LADDAWAN AIEMSOMBOON  and
WUTIPHOL SINTUNAVARAT
LADDAWAN AIEMSOMBOON
Affiliation:
Department of Mathematics and Statistics, Faculty of Science and Technology, Thammasat University Rangsit Center, Pathumthani 12121, Thailand email Laddawan_Aiemsomboon@hotmail.com
WUTIPHOL SINTUNAVARAT*
Affiliation:
Department of Mathematics and Statistics, Faculty of Science and Technology, Thammasat University Rangsit Center, Pathumthani 12121, Thailand email wutiphol@mathstat.sci.tu.ac.th
*
✉wutiphol@mathstat.sci.tu.ac.th
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

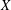Let $X$ be a nonempty subset of a normed space such that 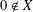$0\notin X$ and 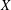$X$ is symmetric with respect to 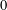$0$ and let 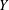$Y$ be a Banach space. We study the generalised hyperstability of the Drygas functional equation

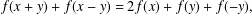$$\begin{eqnarray}f(x+y)+f(x-y)=2f(x)+f(y)+f(-y),\end{eqnarray}$$
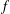where $f$ maps 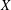$X$ into 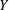$Y$ and 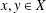$x,y\in X$ with 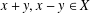$x+y,x-y\in X$. Our first main result improves the results of Piszczek and Szczawińska [‘Hyperstability of the Drygas functional equation’, J. Funct. Space Appl.2013 (2013), Article ID 912718, 4 pages]. Hyperstability results for the inhomogeneous Drygas functional equation can be derived from our results.

Keywords

generalised hyperstabilityDrygas functional equationfixed point theorem

MSC classification

Primary: 39B82: Stability, separation, extension, and related topics
Secondary: 39B62: Functional inequalities, including subadditivity, convexity, etc. 47H14: Perturbations of nonlinear operators 47H10: Fixed-point theorems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 95 , Issue 2 , April 2017 , pp. 269 - 280
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

This work was supported by the Research Professional Development Project under the Science Achievement Scholarship of Thailand (SAST). The second author was supported by the Thailand Research Fund and Office of the Higher Education Commission under grant no. MRG5980242.

References

Aiemsomboon, L. and Sintunavarat, W., ‘On generalized hyperstability of a general linear equation’, Acta Math. Hungar. 149(2) (2016), 413–422.Google Scholar
Bourgin, D. G., ‘Approximately isometric and multiplicative transformations on continuous function rings’, Duke Math. J. 16 (1949), 385–397.Google Scholar
Brzdȩk, J., ‘Stability of additivity and fixed point methods’, Fixed Point Theory Appl. 2013 (2013), Article ID 285, 9 pages.Google Scholar
Brzdȩk, J., ‘Remarks on stability of some inhomogeneous functional equations’, Aequationes Math. 89 (2015), 83–96.Google Scholar
Brzdȩk, J., Chudziak, J. and Páles, Zs., ‘Fixed point approach to stability of functional equations’, Nonlinear Anal. 74 (2011), 6728–6732.CrossRefGoogle Scholar
Brzdȩk, J. and Cieplinski, K., ‘Hyperstability and superstability’, Abstr. Appl. Anal. 2013 (2013), Article ID 401756, 13 pages.CrossRefGoogle Scholar
Drygas, H., ‘Quasi-inner products and their applications’, in: Advances in Multivariate Statistical Analysis (ed. Gupta, K.) (Springer, Netherlands, 1987), 13–30.Google Scholar
Ebanks, B. R., Kannappan, Pl. and Sahoo, P. K., ‘A common generalization of functional equations characterizing normed and quasi-inner-product spaces’, Canad. Math. Bull. 35(3) (1992), 321–327.Google Scholar
Faĭziev, V. A. and Sahoo, P. K., ‘On the stability of Drygas functional equation on groups’, Banach J. Math. Anal. 1(1) (2007), 43–55.CrossRefGoogle Scholar
Faĭziev, V. A. and Sahoo, P. K., ‘Stability of Drygas functional equation on T (3, ℝ)’, Int. J. Math. Stat. 7 (2007), 70–81.Google Scholar
Jung, S. M. and Sahoo, P. K., ‘Stability of a functional equation of Drygas’, Aequationes Math. 64 (2002), 263–273.Google Scholar
Maksa, Gy. and Páles, Zs., ‘Hyperstability of a class of linear functional equations’, Acta Math. Acad. Paedagog. Nyházi. (N.S.) 17 (2001), 107–112.Google Scholar
Piszczek, M., ‘Hyperstability of the general linear functional equation’, Bull. Korean Math. Soc. 52 (2015), 1827–1838.Google Scholar
Piszczek, M. and Szczawińska, J., ‘Hyperstability of the Drygas functional equation’, J. Funct. Spaces Appl. 2013 (2013), Article ID 912718, 4 pages.CrossRefGoogle Scholar
Yang, D., ‘Remarks on the stability of Drygas equation and the Pexider-quadratic equation’, Aequationes Math. 64 (2004), 108–116.CrossRefGoogle Scholar
Zhang, D., ‘On hyperstability of generalised linear functional equations in several variables’, Bull. Aust. Math. Soc. 92 (2015), 259–267.CrossRefGoogle Scholar
Zhang, D., ‘On Hyers–Ulam stability of generalized linear functional equation and its induced Hyers–Ulam programming problem’, Aequationes Math. 90 (2016), 559–568.CrossRefGoogle Scholar