Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T17:07:54.468Z Has data issue: false hasContentIssue false
  • English
  • Français

UNCERTAINTY PRINCIPLES CONNECTED WITH THE MÖBIUS INVERSION FORMULA

Part of: Multiplicative number theory Elementary number theory

Published online by Cambridge University Press:  25 January 2013

PAUL POLLACK  and
CARLO SANNA
PAUL POLLACK*
Affiliation:
Department of Mathematics, University of Georgia, Athens, Georgia 30602, USA
CARLO SANNA
Affiliation:
Department of Mathematics, Università degli Studi di Torino, Turin, Italy email carlo.sanna.dev@gmail.com
*
✉pollack@uga.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Two arithmetic functions 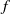$f$ and 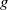$g$ form a Möbius pair if 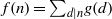$f(n)= {\mathop{\sum }\nolimits}_{d\mid n} g(d)$ for all natural numbers $n$. In that case, 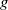$g$ can be expressed in terms of 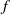$f$ by the familiar Möbius inversion formula of elementary number theory. In a previous paper, the first-named author showed that if the members 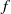$f$ and 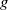$g$ of a Möbius pair are both finitely supported, then both functions vanish identically. Here we prove two significantly stronger versions of this uncertainty principle. A corollary is that in a nonzero Möbius pair, one cannot have both 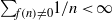${\mathop{\sum }\nolimits}_{f(n)\not = 0} 1/ n\lt \infty $ and 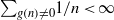${\mathop{\sum }\nolimits}_{g(n)\not = 0} 1/ n\lt \infty $.

Keywords

Möbius inversionMöbius transformuncertainty principlesets of multiples

MSC classification

Secondary: 11A25: Arithmetic functions; related numbers; inversion formulas 11N37: Asymptotic results on arithmetic functions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 3 , December 2013 , pp. 460 - 472
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Erdős, P., ‘On the density of abundant numbers’, J. Lond. Math. Soc. 9 (1934), 278–282.Google Scholar
Erdős, P. and Wagstaff, S. S. Jr, ‘The fractional parts of the Bernoulli numbers’, Illinois J. Math. 24 (1980), 104–112.Google Scholar
Hall, R. R., Sets of Multiples, Cambridge Tracts in Mathematics, 118 (Cambridge University Press, Cambridge, 1996).Google Scholar
Heilbronn, H. A., ‘On an inequality in the elementary theory of numbers’, Proc. Cambridge Philos. Soc. 33 (1937), 207–209.Google Scholar
Kronecker, L., ‘Quelques remarques sur la détermination des valeurs moyennes’, C. R. Acad. Sci. Paris 103 (1887), 980–987.Google Scholar
Landau, E., Handbuch der Lehre von der Verteilung der Primzahlen. 2 Bände, 2nd edn. (Chelsea Publishing Co., New York, 1953).Google Scholar
Montgomery, H. L. and Vaughan, R. C., Multiplicative Number Theory. I. Classical Theory, Cambridge Studies in Advanced Mathematics, 97 (Cambridge University Press, Cambridge, 2007).Google Scholar
Pollack, P., Not Always Buried Deep (American Mathematical Society, Providence, RI, 2009).CrossRefGoogle Scholar
Pollack, P., ‘The Möbius transform and the infinitude of primes’, Elem. Math. 66 (2011), 118–120.CrossRefGoogle Scholar
Pomerance, C. and Sárközy, A., ‘On homogeneous multiplicative hybrid problems in number theory’, Acta Arith. 49 (1988), 291–302.Google Scholar
Rohrbach, H., ‘Beweis einer zahlentheoretischen Ungleichung’, J. reine angew. Math. 177 (1937), 193–196.CrossRefGoogle Scholar
Wintner, A., Eratosthenian Averages (Waverly Press, Baltimore, 1943).Google Scholar