Published online by Cambridge University Press: 11 November 2015
We prove the unimodality of some coloured 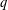 $q$-Eulerian polynomials, which involve the flag excedances, the major index and the fixed points on coloured permutation groups, via two recurrence formulas. In particular, we confirm a recent conjecture of Mongelli about the unimodality of the flag excedances over type B derangements. Furthermore, we find the coloured version of Gessel’s hook factorisation, which enables us to interpret these two recurrences combinatorially. We also provide a combinatorial proof of a symmetric and unimodal expansion for the coloured derangement polynomial, which was first established by Shin and Zeng using continued fractions.
$q$-Eulerian polynomials, which involve the flag excedances, the major index and the fixed points on coloured permutation groups, via two recurrence formulas. In particular, we confirm a recent conjecture of Mongelli about the unimodality of the flag excedances over type B derangements. Furthermore, we find the coloured version of Gessel’s hook factorisation, which enables us to interpret these two recurrences combinatorially. We also provide a combinatorial proof of a symmetric and unimodal expansion for the coloured derangement polynomial, which was first established by Shin and Zeng using continued fractions.