Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T13:42:14.276Z Has data issue: false hasContentIssue false
  • English
  • Français

THE UNIQUE CONTINUATION PROPERTY OF 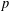$p$-HARMONIC FUNCTIONS ON THE HEISENBERG GROUP

Part of: Partial differential equations Close-to-elliptic equations and systems Elliptic equations and systems

Published online by Cambridge University Press:  12 November 2018

HAIRONG LIU Open the ORCID record for HAIRONG LIU [Opens in a new window] ,
FANG LIU  and
HUI WU
HAIRONG LIU*
Affiliation:
School of Science, Nanjing Forestry University, Nanjing, 210037, PR China email hrliu@njfu.edu.cn
FANG LIU
Affiliation:
Department of Mathematics, Nanjing University, Nanjing, 210093, PR China email sdqdlf78@126.com
HUI WU
Affiliation:
School of Mathematical Sciences, Qufu Normal University, Qufu, 273165, PR China email wuhui8668@126.com
*
✉hrliu@njfu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We introduce an Almgren frequency function of the sub-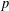$p$-Laplace equation on the Heisenberg group to establish a doubling estimate under the assumption that the frequency function is locally bounded. From this, we obtain some partial results on unique continuation for the sub-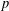$p$-Laplace equation.

Keywords

Heisenberg groupfrequency functionunique continuation principle

MSC classification

Primary: 35B60: Continuation and prolongation of solutions
Secondary: 35H20: Subelliptic equations 35J70: Degenerate elliptic equations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 2 , April 2019 , pp. 219 - 230
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author was supported by the NSFC (Grant No. 11401310), the Qing Lan Project of Jiangsu Province and the overseas research program of Jiangsu Province. The second author was supported by the NSFC (Grant No. 11501292).

References

Adamowicz, T. and Warhurst, B., ‘Three-spheres theorems for subelliptic quasilinear equations in Carnot groups of Heisenberg-type’, Proc. Amer. Math. Soc. 144 (2016), 4291–4302.Google Scholar
Almgren, F. J. Jr, ‘Dirichlet’s problem for multiple valued functions and the regularity of mass minimizing integral currents’, in: Minimal Submanifolds and Geodesics (ed. Obata, M.) (North-Holland, Amsterdam, 1979), 1–6.Google Scholar
Bellaïche, A., ‘The tangent space in sub-Riemannian geometry’, Progr. Math. 144 (1996), 1–78.Google Scholar
Bonfiglioli, A., Lanconelli, E. and Uguzzoni, F., Stratified Lie Groups and Potential Theory for their Sub-Laplacians, Springer Monographs in Mathematics (Springer, Berlin–Heidelberg–New York, 2007).Google Scholar
Capogna, L., ‘Regularity of quasi-linear equations in the Heisenberg group’, Comm. Pure Appl. Math. 50 (1997), 867–889.Google Scholar
Domokos, A., ‘Differentiability of solutions for the non-degenerate p-Laplacian in the Heisenberg group’, J. Differential Equations 204 (2004), 439–470.Google Scholar
Evans, L., ‘A new proof of local C 1, 𝛼 regularity for solutions of certain degenerate elliptic p.d.e.’, J. Differential Equations 45 (1982), 356–373.10.1016/0022-0396(82)90033-XGoogle Scholar
Garofalo, N. and Lanconelli, E., ‘Frequency functions on the Heisenberg group, the uncertainty principle and unique continuation’, Ann. Inst. Fourier 44 (1990), 313–356.Google Scholar
Garofalo, N. and Lin, F., ‘Unique continuation for elliptic operators: a geometric-variational approach’, Comm. Pure Appl. Math. 40 (1987), 347–366.Google Scholar
Garofalo, N. and Vassilev, D., ‘Strong unique continuation properties of generalized Baouendi–Grushin operators’, Comm. Partial Differential Equations 32 (2007), 643–663.Google Scholar
Granlund, S. and Marola, N., ‘On the problem of unique continuation for the p-Laplace equation’, Nonlinear Anal. Theory Methods Appl. 101 (2014), 89–97.Google Scholar
Greiner, P. C., ‘Spherical harmonics on the Heisenberg group’, Canad. Math. Bull. 23 (1980), 383–396.Google Scholar
Guo, C. and Kar, M., ‘Quantitative uniqueness estimates for p-Laplace type equations in the plane’, Nonlinear Anal. Theory Methods Appl. 143 (2016), 19–44.Google Scholar
Hörmander, L., ‘Hypoelliptic second-order differential equations’, Acta Math. 119 (1967), 147–171.Google Scholar
Lewis, J. L., ‘Smoothness of certain degenerate elliptic equations’, Proc. Amer. Math. Soc. 80 (1980), 259–265.Google Scholar
Lin, F. and Yang, X., Geometric Measure Theory: An Introduction (International Press, Boston, MA, 2002).Google Scholar
Liu, H. and Yang, X., ‘Strong unique continuation of sub-elliptic operator on the Heisenberg group’, Chin. Ann. Math. Ser. B 34 (2013), 461–478.Google Scholar
Lu, G., ‘Weighted Poincaré and Sobolev inequalities for vector fields satisfying Hörmander’s condition and applications’, Rev. Mat. Iberoam. 8 (1992), 367–439.Google Scholar
Manfredi, J. J., ‘ p-harmonic functions in the plane’, Proc. Amer. Math. Soc. 103 (1988), 473–479.Google Scholar
Mukherjee, S. and Zhong, X., ‘ $C^{1,\unicode[STIX]{x1D6FC}}$ -regularity for variational problems in the Heisenberg group’, Preprint, 2017, arXiv:1711.04671v2.Google Scholar
Ricciotti, D., p-Laplace Equation in the Heisenberg Group, Regularity of Solutions, Springer Briefs in Mathematics (Springer, Cham, Switzerland, 2015).Google Scholar
Ricciotti, D., ‘On the C 1, 𝛼 regularity of p-harmonic functions in the Heisenberg group’, Proc. Amer. Math. Soc. 146 (2018), 2937–2952.10.1090/proc/13961Google Scholar
Rothschild, L. P. and Stein, E. M., ‘Hypoelliptic differential operators and nilpotent groups’, Acta Math. 137 (1976), 247–320.Google Scholar
Zhong, X., ‘Regularity for variational problems in the Heisenberg group’, Preprint, 2017, arXiv:1711.03284.Google Scholar