Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-29T05:26:00.240Z Has data issue: false hasContentIssue false
  • English
  • Français

A UNIQUE REPRESENTATION BI-BASIS FOR THE INTEGERS. II

Part of: Sequences and sets

Published online by Cambridge University Press:  08 January 2016

MIN TANG
MIN TANG*
Affiliation:
School of Mathematics and Computer Science, Anhui Normal University, Wuhu 241003, China email tmzzz2000@163.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For 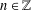$n\in \mathbb{Z}$ and 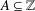$A\subseteq \mathbb{Z}$, define 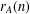$r_{A}(n)$ and 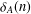${\it\delta}_{A}(n)$ by 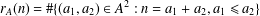$r_{A}(n)=\#\{(a_{1},a_{2})\in A^{2}:n=a_{1}+a_{2},a_{1}\leq a_{2}\}$ and 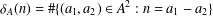${\it\delta}_{A}(n)=\#\{(a_{1},a_{2})\in A^{2}:n=a_{1}-a_{2}\}$. We call 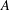$A$ a unique representation bi-basis if 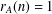$r_{A}(n)=1$ for all 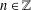$n\in \mathbb{Z}$ and 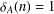${\it\delta}_{A}(n)=1$ for all 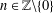$n\in \mathbb{Z}\setminus \{0\}$. In this paper, we prove that there exists a unique representation bi-basis 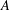$A$ such that 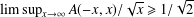$\limsup _{x\rightarrow \infty }A(-x,x)/\sqrt{x}\geq 1/\sqrt{2}$.

Keywords

unique representation bi-basisSidon set

MSC classification

Primary: 11B13: Additive bases, including sumsets
Secondary: 11B34: Representation functions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 1 , August 2016 , pp. 1 - 6
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Chen, Y. G., ‘A problem on unique representation bases’, European J. Combin. 28 (2007), 33–35.CrossRefGoogle Scholar
Cilleruelo, J. and Nathanson, M. B., ‘Perfect difference sets constructed from Sidon sets’, Combinatorica 28 (2008), 401–414.CrossRefGoogle Scholar
Cilleruelo, J. and Nathanson, M. B., ‘Dense sets of integers with prescribed representation functions’, European J. Combin. 34 (2013), 1297–1306.CrossRefGoogle Scholar
Lee, J., ‘Infinitely often dense bases for the integers with a prescribed representation function’, Integers 10 (2010), 299–307.CrossRefGoogle Scholar
Nathanson, M. B., ‘Unique representation bases for integers’, Acta Arith. 108 (2003), 1–8.CrossRefGoogle Scholar
Nathanson, M. B., ‘Every function is the representation function of an additive basis for the integers’, Port. Math. 62 (2005), 55–72.Google Scholar
Tang, M., ‘Dense sets of integers with a prescribed representation function’, Bull. Aust. Math. Soc. 84 (2011), 40–43.CrossRefGoogle Scholar
Xiong, R. and Tang, M., ‘Unique representation bi-basis for the integers’, Bull. Aust. Math. Soc. 89 (2014), 460–465.CrossRefGoogle Scholar