Article contents
Univalent functions with univalent Gelfond-Leontev derivatives
Published online by Cambridge University Press: 17 April 2009
Abstract
Let 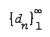 be a nondecreasing sequence of positive numbers. We consider Gelfond-Leontev derivative Df(z), of a function
be a nondecreasing sequence of positive numbers. We consider Gelfond-Leontev derivative Df(z), of a function 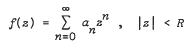 , defined by
, defined by 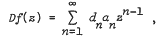 for univalence and growth properties, and extend some results of Shah and Trimble. Set en = {d1d2 … dn), n≥l, e0 = 1,
for univalence and growth properties, and extend some results of Shah and Trimble. Set en = {d1d2 … dn), n≥l, e0 = 1, 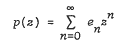 . Let r be the radius of convergence of p(z). We state parts of Theorem 1 and Corollaries. Let f and all Dkf, k = 1, 2,…, be analytic and univalent in the unit disk U. Then
. Let r be the radius of convergence of p(z). We state parts of Theorem 1 and Corollaries. Let f and all Dkf, k = 1, 2,…, be analytic and univalent in the unit disk U. Then
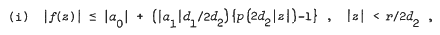
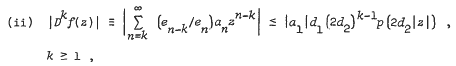
(iii) if p is entire and of growth (ρ, T) then f must be entire and of growth not exceeding (ρ, 2d2T),
(iv) if D corresponds to the shift operator (dn ≡ l), then 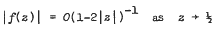 .
.
Another class of functions is defined by a condition of the form |an+1/an| ≤ bn+1/dn+1, where 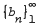 is a sequence of positive numbers satisfying and inequality, and it is shown that all functions in this class along with all their Gelfond–Leontev successive derivatives are regular and univalent in U. An extension of the definition of a linear invariant family is given and results analogous to (i) and (ii) are stated.
is a sequence of positive numbers satisfying and inequality, and it is shown that all functions in this class along with all their Gelfond–Leontev successive derivatives are regular and univalent in U. An extension of the definition of a linear invariant family is given and results analogous to (i) and (ii) are stated.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1984
References
- 2
- Cited by


