Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
KUANG, MEIJUN
HUANG, GUIHUA
and
DENG, HANYUAN
2016.
Some sufficient conditions for Hamiltonian property in terms of Wiener-type invariants.
Proceedings - Mathematical Sciences,
Vol. 126,
Issue. 1,
p.
1.
LIU, RUIFANG
DU, XUE
and
JIA, HUICAI
2016.
WIENER INDEX ON TRACEABLE AND HAMILTONIAN GRAPHS.
Bulletin of the Australian Mathematical Society,
Vol. 94,
Issue. 3,
p.
362.
Feng, Lihua
Zhu, Xiaomin
and
Liu, Weijun
2017.
Wiener index, Harary index and graph properties.
Discrete Applied Mathematics,
Vol. 223,
Issue. ,
p.
72.
Zhou, Qiannan
Wang, Ligong
and
Lu, Yong
2018.
Wiener index and Harary index on Hamilton-connected graphs with large minimum degree.
Discrete Applied Mathematics,
Vol. 247,
Issue. ,
p.
180.
Zhou, Qiannan
Wang, Ligong
and
Lu, Yong
2018.
Some sufficient conditions on k-connected graphs.
Applied Mathematics and Computation,
Vol. 325,
Issue. ,
p.
332.
An, Mingqiang
Zhang, Yinan
Das, Kinkar Ch.
and
Xiong, Liming
2019.
Reciprocal degree distance and graph properties.
Discrete Applied Mathematics,
Vol. 258,
Issue. ,
p.
1.
Chen, Lian
Mehboob, Abid
Ahmad, Haseeb
Nazeer, Waqas
Hussain, Muhammad
and
Farahani, M. Reza
2019.
Hosoya and Harary Polynomials ofTOX(n),RTOX(n),TSL(n)andRTSL(n).
Discrete Dynamics in Nature and Society,
Vol. 2019,
Issue. ,
p.
1.
Wang, Dejun
Ahmad, Haseeb
and
Nazeer, Waqas
2020.
Hosoya and Harary polynomials of TUC4 nanotube.
Mathematical Methods in the Applied Sciences,
Cancan, Murat
Hussain , Muhammad
and
Ahmad , Haseeb
2020.
Distance and eccentricity based polynomials and indices of m−level Wheel graph.
Proyecciones (Antofagasta),
Vol. 39,
Issue. 4,
p.
869.
Lu, Yong
and
Zhou, Qiannan
2021.
On sufficient topological indices conditions for properties of graphs.
Journal of Combinatorial Optimization,
Vol. 41,
Issue. 2,
p.
487.
An, Mingqiang
2022.
The first Zagreb index, reciprocal degree distance and Hamiltonian-connectedness of graphs.
Information Processing Letters,
Vol. 176,
Issue. ,
p.
106247.
Su, Guifu
Wang, Shuai
Du, Junfeng
Gao, Mingjing
Das, Kinkar Chandra
and
Shang, Yilun
2022.
Sufficient Conditions for a Graph to Be ℓ-Connected, ℓ-Deficient, ℓ-Hamiltonian and ℓ−-Independent in Terms of the Forgotten Topological Index.
Mathematics,
Vol. 10,
Issue. 11,
p.
1802.
Liu, Yonghong
Rauf, Abdul
AdnanAslam
Ishaq, Saira
Issa, Abudulai
and
Malik, Sarfraz Nawaz
2022.
Computing Wiener and Hyper-Wiener Indices of Zero-Divisor Graph of
ℤ
ℊ
3
×
ℤ
I
1
I
2
.
Journal of Function Spaces,
Vol. 2022,
Issue. ,
p.
1.
An, Mingqiang
Zhang, Yinan
Das, Kinkar Chandra
and
Shang, Yilun
2023.
On reciprocal degree distance of graphs.
Heliyon,
Vol. 9,
Issue. 7,
p.
e17914.
Kori, Rajkaran
Prasad, Abhyendra
and
Upadhyay, Ashish K.
2023.
Reciprocal degree distance and Hamiltonian properties of graphs.
Operations Research Letters,
Vol. 51,
Issue. 6,
p.
623.
An, Mingqiang
Zhang, Yinan
and
Yan, Huiya
2024.
Sufficient conditions for k-leaf-connected graphs in terms of the first Zagreb index, the reciprocal degree distance and the forgotten topological index.
Discrete Applied Mathematics,
Vol. 351,
Issue. ,
p.
74.
Subashini, G.
Kannan, K.
and
Menaga, A.
2024.
Exponential Wiener index of some silicate networks.
Scientific Reports,
Vol. 14,
Issue. 1,
Kori, Rajkaran
Prasad, Abhyendra
and
Upadhyay, Ashish K.
2025.
On sufficient condition for t-toughness of a graph in terms of eccentricity-based indices.
National Academy Science Letters,
Vol. 48,
Issue. 1,
p.
73.
 $n$ is at most
$n$ is at most 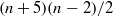 $(n+ 5)(n- 2)/ 2$, then it is traceable.
$(n+ 5)(n- 2)/ 2$, then it is traceable.

