Hostname: page-component-76c49bb84f-7l7zb Total loading time: 0 Render date: 2025-07-12T16:35:11.939Z Has data issue: false hasContentIssue false
  • English
  • Français

X-ROKHLIN PROPERTY FOR ACTIONS OF COUNTABLE DISCRETE GROUPS

Part of: Selfadjoint operator algebras Linear spaces and algebras of operators

Published online by Cambridge University Press:  04 July 2025

XIAOCHUN FANG Open the ORCID record for XIAOCHUN FANG [Opens in a new window]  and
XIN CAO Open the ORCID record for XIN CAO [Opens in a new window]
XIAOCHUN FANG
Affiliation:
School of Mathematical Sciences, Key Laboratory of Intelligent Computing and Applications (Ministry of Education), https://ror.org/03rc6as71Tongji University, Shanghai 200092, PR China e-mail: xfang@tongji.edu.cn
XIN CAO*
Affiliation:
School of Mathematical Sciences, Key Laboratory of Intelligent Computing and Applications (Ministry of Education), https://ror.org/03rc6as71Tongji University, Shanghai 200092, PR China
*
e-mail: 2111153@tongji.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

We extend the definition of the X-Rokhlin property to countable discrete groups and prove some permanence properties. If the action of a countable discrete group on X is free and minimal and the action of this group on the separable simple 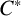$C^*$-algebra has the X-Rokhlin property, then the reduced crossed product is simple.

Keywords

C*-algebracrossed productRokhlin property

MSC classification

Primary: 47L65: Crossed product algebras (analytic crossed products)
Secondary: 46L05: General theory of $C^*$-algebras

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 11
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Amini, M., Golestani, N., Jamali, S. and Phillips, N. C., ‘Finite group and integer actions on simple tracially $\mathcal{Z}$ -absorbing ${C}^{\ast }$ -algebras’, J. Operator Theory 92(2) (2024), 505–547.10.7900/jot.2022nov02.2417CrossRefGoogle Scholar
Choi, M. D. and Effros, E. G., ‘The completely positive lifting problem for ${C}^{\ast }$ -algebras’, Ann. of Math. (2) 104(3) (1976), 585–609.10.2307/1970968CrossRefGoogle Scholar
Gardella, E., ‘Rokhlin dimension for compact group actions’, Indiana Univ. Math. J. 66(2) (2017), 659–703.10.1512/iumj.2017.66.5951CrossRefGoogle Scholar
Gardella, E., ‘Regularity properties and Rokhlin dimension for compact group actions’, Houston J. Math. 43(3) (2017), 861–889.Google Scholar
Hirshberg, I. and Phillips, N. C., ‘Rokhlin dimension: obstructions and permanence properties’, Doc. Math. 20 (2015), 199–236.10.4171/dm/489CrossRefGoogle Scholar
Hirshberg, I., Szabó, G., Winter, W. and Wu, J., ‘Rokhlin dimension for flows’, Comm. Math. Phys. 353(1) (2017), 253–316.10.1007/s00220-016-2762-0CrossRefGoogle Scholar
Hirshberg, I., Winter, W. and Zacharias, J., ‘Rokhlin dimension and ${C}^{\ast }$ -dynamics’, Comm. Math. Phys. 335(2) (2015), 637–670.10.1007/s00220-014-2264-xCrossRefGoogle Scholar
Izumi, M., ‘Finite group actions on ${C}^{\ast }$ -algebras with the Rokhlin property. I’, Duke Math. J. 122(2) (2004), 233–280.10.1215/S0012-7094-04-12221-3CrossRefGoogle Scholar
Izumi, M., ‘Finite group actions on ${C}^{\ast }$ -algebras with the Rokhlin property. II’, Adv. Math. 184(1) (2004), 119–160.10.1016/S0001-8708(03)00140-3CrossRefGoogle Scholar
Kishimoto, A., ‘Outer automorphisms and reduced crossed products of simple ${C}^{\ast }$ -algebras’, Comm. Math. Phys. 81(3) (1981), 429–435.10.1007/BF01209077CrossRefGoogle Scholar
Phillips, N. C., ‘The tracial Rokhlin property for actions of finite groups on ${C}^{\ast }$ -algebras’, Amer. J. Math. 133(3) (2011), 581–636.10.1353/ajm.2011.0016CrossRefGoogle Scholar
Sureshkumar, M. and Vaidyanathan, P., ‘Rokhlin dimension: permanence properties and ideal separation’, Groups Geom. Dyn., to appear; doi:10.4171/GGD/825.CrossRefGoogle Scholar
Szabó, G., Wu, J. and Zacharias, J., ‘Rokhlin dimension for actions of residually finite groups’, Ergodic Theory Dynam. Systems 39(8) (2019), 2248–2304.10.1017/etds.2017.113CrossRefGoogle Scholar