A construction due to Reilly is extended to show that there is a correspondence between compatible tight Riesz orders on ZX and non-principal filters on X. The maximal compatible tight Riesz orders are in one-to-one correspondence with non-principal ultra-filters, and are dual prime subsets of the positive set of ZX. Conversely every dual prime algebraic Riesz order is maximal.

If an optimal solution exists for a nonlinear fractional programming problem, then this solution is shown to be obtainable by solving two associated programming problems whose objective functions are no longer fractional. A certain restriction is assumed on the constraint sets of the latter problems. This result includes various known theorems as special cases.

Complicated groups of exponent four have been constructed from the ring of polynomials in associating non-commuting indeterminates with coefficients from the field of two elements. The justification of these constructions depends on a computational reduction result. In this note a further reduction is obtained. The expressions involved seem to have an interesting combinatorial structure.

We consider a method by which players in a continuous N-person game can arrive at a Pareto optimal solution by a trial process. The process has a number of novel features. Firstly, it is assumed that the players do not know the payoff functions. Secondly, the players are assumed to act quite independently. In spite of this lack of information and lack of cooperation, the players eventually arrive at what is usually regarded as a cooperative solution. The process is a model of the accounting procedures used by firms, and the results predict approach to an equilibrium state of a market model. Proofs are given only in outline here.

A boolean space is a compact Hausdorff space which is zero-dimensional. In this paper, a boolean space X is characterized in terms of its ring of real-valued functions C(X). The result is sharpened for the case when X is an F-space (every finitely generated ideal of C(X) is principal).

We announce a number of results on the existence of solutions of nonlinear elliptic boundary value problems in the case where the dominating linear part is not invertible. Our theorems improve recent results of Landesman and Lazer, and Williams.

D.L. Berman has proved several divergence theorems about “extended” Hermite-Fejér interpolation on the Chebyshev nodes of the first kind. These are surprising in light of the classical convergence theorem of L. Fejér concerning ordinary Hermite-Fejér interpolation on these nodes. However there is one case which has been neglected so far: the case of quasi-Hermite-Fejér interpolation on these nodes. In this paper it is proved that quasi-Hermite-Fejér interpolation polynomials on the Chebyshev nodes converge uniformly to the continuous function being interpolated. In addition, an estimate for the rate of convergence is established.

Let the group T be the direct product of groups Si (i = 1, … r) where for a given group Ai, Si is the direct product of ni factors Ai × Ai × … × Ai. Let B be a group that has a faithful permutation representation Γi of degree ni. (i = 1, …, r). Consider G, the split extension of T by B defined by letting B act on T as follows.

Each Si is normal in G. If 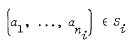and b ∈ B then 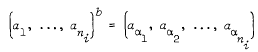where 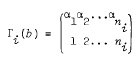. It is proved that if T is an M-group and all subgroups of B are M-groups, then G is an M-group. This is a generalisation of a result of Gary M. Seitz, Math. Z. 110 (1969), 101–122, who proved the particular case where r = 1 and Γ1 is the regular representation of B.

We prove that if E is a Banach space which has a subspace G such that the conjugate space G* contains a proper norm closed linear subspace V of characteristic 1, then E** is not smooth and there exist in πE(E) points of non-smoothness for E**, where πE: E → E** is the canonical embedding. We show that the spaces E having such a subspace G constitute a large proper subfamily of the family of all non-reflexive Banach spaces.

It is shown that the correspondence which associates with each radical class τ of abelian groups the (radical) class of prime radical rings with additive groups in τ gives a complete classification of those radical classes of rings which are determined (as lower radicals) by zerorings.

The negative answer by Novikov and Adyan to the Burnside question (is every finitely generated group of finite exponent finite?) still leaves open some cases, in particular, all 2-power exponents. Some reduction results are known. In this note we present another kind of reduction result.

This paper is a continuation of the study of the boundedness operator δ. By determination of the congruences (that is, collapsings) of the smallest lattice containing δ and closed under application of δ, a nev classification of all topological spaces is obtained according to boundedness criteria.

The classical formulae for Fredholm integral equations, including expansions in terms of eigenfunctions such as Mercer's Theorem are extended to square-integrable kernels on an arbitrary measure space.

When a totally-ordered set Ω has no points fixed by all automorphisms ve equip Ω with the support topology which has fixed-sets of automorphisms as basic closed sets. There is a mapping from Ω into the set of prime dual ideals of the lattice Φ(Ω) of basic closed sets and this allows us to classify the points of Ω as excellent, isolated, static, or extraordinary. There is an action of the group of automorphisms of Ω on the lattice Φ(Ω) and this allows us to see that automorphisms of Ω preserve the prime dual ideal classification of points of Ω. When the empty set is a basic closed subset of Ω the dual spectrum of Φ(Ω) is a compact T0 space (Hausdorff when all points of Ω are excellent) containing Ω as a dense subspace and allowing an extension of each automorphism of Ω ťo a homeomorphism of the dual spectrum.

An explicit construction is given for a primitive group ring, together with an explicit construction of a faithful irreducible module for it.

The oscillatory behaviour of the solutions of a functional differential equation, of more general form than an equation arising from in industrial problem, is examined. The question of whether one can maintain the oscillatory properties of this equation by adding a forcing term is also answered. The results obtained extend already known results on the subject and complete the relevant literature.

Certain new combinatorial numbers which arise in the counting of finite topologies are introduced and formulae obtained. These numbers are used to obtain a known formula for tn, the number of labelled topologies on n points in terms of the Stirling numbers S(n, p) and dn, the number of labelled T0-topologies on n points. The numbers dn are computed for n ≤ 5 with the the help of a method of Comtet (1966) (which seems to have been missed by later authors), reinterpreted for transitive digraphs.

Let G be a Hausdorff locally compact abelian group. The author has shown (Bull. Austral. Math. Soc. 10 (1974), 59–66) that, given ε > 0 and a certain base {Vi}i∈I of symmetric open neighbourhoods of zero, the algebra L1(G) admits a bounded positive approximate unit {ki}i∈I such that for every p–th integrable function f on G,

where ω(p; f; Vi) denotes the mean modulus of continuity with exponent p of f. The purpose of this paper is to obtain {ki}i∈I (as above) with a simple dependence of supp on {ki}i∈I on Vi; this is achieved for finite products and homomorphic images of groups for which such a simple dependence is known. The results obtained are used to give a simplified proof of the classical Jackson's Theorem for the circle group, and an analogue of this theorem for the a-adic solenoid.

It is shown that if q is a prime power then there exists a circulant weighing matrix of order q2 + q + 1 with q2 nonzero elements per row and column.

This result allows the bound N to be lowered in the theorem of Geramita and Wallis that “given a square integer k there exists an integer N dependent on k such that weighing matrices of weight k and order n and orthogonal designs (1, k) of order 2n exist for every n > N”.

A theoretical study is made of the free periods of oscillation of a global layer of inviscid, incompressible fluid under the action of gravitational and Coriolis forces. The leading approximations to the eigenvalues are found to be sensitive to variations in the Froude number and also to the shape of the globe. It is shown that for oceanic and atmospheric motions displaying essentially the same features as the model, it is not sufficient to consider the motion as horizontally non-divergent.