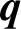 $\boldsymbol {q}$
-SUPERCONGRUENCES MODULO THE CUBE OF A CYCLOTOMIC POLYNOMIAL
$\boldsymbol {q}$
-SUPERCONGRUENCES MODULO THE CUBE OF A CYCLOTOMIC POLYNOMIAL
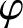 $\varphi $
-AMENABILITY OF DUAL BANACH ALGEBRAS
$\varphi $
-AMENABILITY OF DUAL BANACH ALGEBRAS
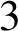 $3$
-MANIFOLDS IN
$3$
-MANIFOLDS IN
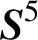 $\boldsymbol {S}^5$
$\boldsymbol {S}^5$